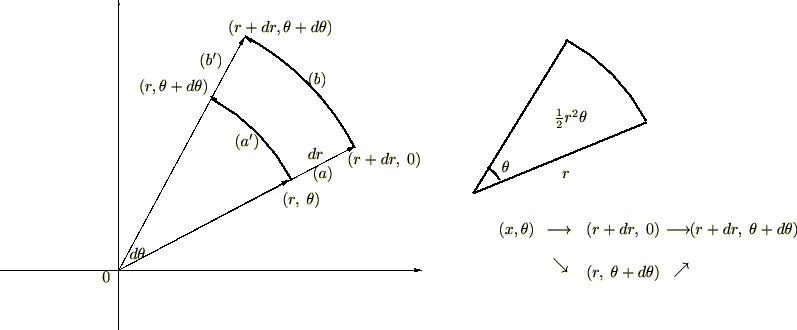�����ϕ��w�ꗗ
���̃`���v�^�[�ł͔����ϕ��ɂ������{�I�Ȍv�Z���炻���W�������Δ����A����ɂ͈�ϐ����̐ϕ��A2�d�ϕ��Ȃǂ̏d�ϕ��Ɋւ�����Ƃ��̉�@�Ȃǂɂ��ďڂ����������Ă����܂��B
�����ϕ��w�L���ꗗ
����
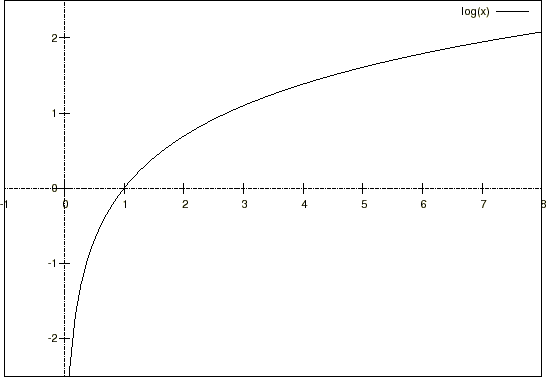 ���̓����ƌĂт܂��B�\�L�̎d���́A�ȂǂƏ����܂��B��L�͉̂p��̂��痈�Ă���͂�����Ȃ��ɋ߂Â���Ƃ����Ӗ���\���ŏI�I�ɂ͂��̂�������Ƃ������Ƃ��Ӗ����Ă��܂��B
���̓����ƌĂт܂��B�\�L�̎d���́A�ȂǂƏ����܂��B��L�͉̂p��̂��痈�Ă���͂�����Ȃ��ɋ߂Â���Ƃ����Ӗ���\���ŏI�I�ɂ͂��̂�������Ƃ������Ƃ��Ӗ����Ă��܂��B
����
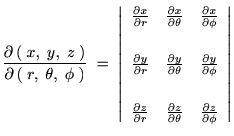 2�̕ϐ�������ꍇ�̊��P�̎��̒��ɂQ�̕ϐ�������ꍇ�̊����l���Ă݂܂��傤�B�ϐ��͂Q����̂ŁA���̂Ƃ��̔����̎d���ɂ͎��̂Q��ނ���܂��B�����Δ����A�܂��͕Γ����Ƃ����A�g�h�͕���ɂ���ϐ��ŕΔ�������Ƃ����Ӗ��̋L���ł��B��ʓI�ɂ́g���E���h�h�ȂǂƂ����Ăѕ������܂��B
2�̕ϐ�������ꍇ�̊��P�̎��̒��ɂQ�̕ϐ�������ꍇ�̊����l���Ă݂܂��傤�B�ϐ��͂Q����̂ŁA���̂Ƃ��̔����̎d���ɂ͎��̂Q��ނ���܂��B�����Δ����A�܂��͕Γ����Ƃ����A�g�h�͕���ɂ���ϐ��ŕΔ�������Ƃ����Ӗ��̋L���ł��B��ʓI�ɂ́g���E���h�h�ȂǂƂ����Ăѕ������܂��B
��ϐ����̐ϕ�
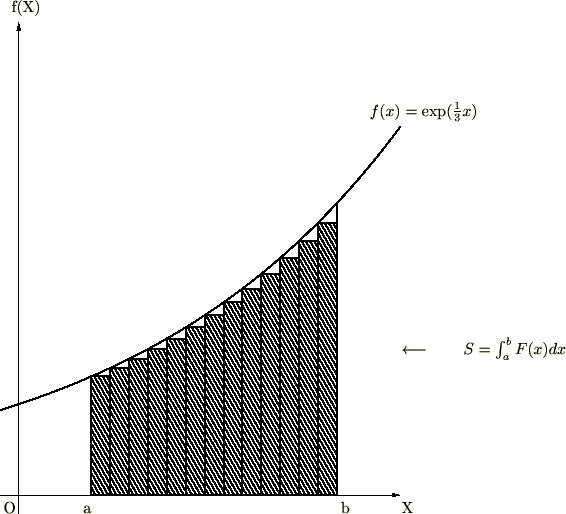 (1.1)��s��ϕ��A(1.2)�̂ق����ϕ��Ƃ����܂��B�ŏ��̕����ɂłĂ���g�h�̓C���e�O�����Ƃ����ϕ����̂��̂��Ӗ����܂��B����ϕ����ł���͂��̏ꍇ�Őϕ����Ȃ���Ȃ�Ȃ��Ƃ������Ƃ��Ӗ����Ă��܂��B
(1.1)��s��ϕ��A(1.2)�̂ق����ϕ��Ƃ����܂��B�ŏ��̕����ɂłĂ���g�h�̓C���e�O�����Ƃ����ϕ����̂��̂��Ӗ����܂��B����ϕ����ł���͂��̏ꍇ�Őϕ����Ȃ���Ȃ�Ȃ��Ƃ������Ƃ��Ӗ����Ă��܂��B
2�d�ϕ�
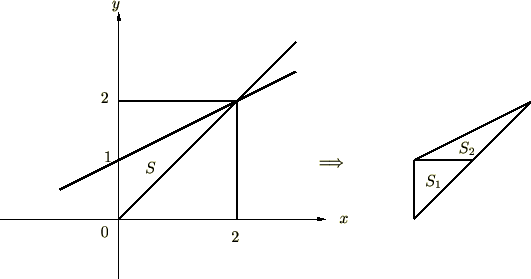 �d�ϕ��|�l�����Ƃ��̎菇�ϕ��̎��ɂ����Ă̔����ʐϗv�f�͑S�Z�N�V�����ɂ����Ď����ꂽ�ɍ��W�ƃf�J���g�̂Q��ނ��������A�ǂ�����g���ċ��߂邩�͋��߂�ʐς̌`�ɂ���Ă��܂��g��������K�v������܂��B�����������Ƃ�O��ɁA���Ɏ������}�`�̖ʐς��d�ϕ��̎����g���ċ��߂Ă݂܂��傤�B�܂����߂�ϕ��̈�...
�d�ϕ��|�l�����Ƃ��̎菇�ϕ��̎��ɂ����Ă̔����ʐϗv�f�͑S�Z�N�V�����ɂ����Ď����ꂽ�ɍ��W�ƃf�J���g�̂Q��ނ��������A�ǂ�����g���ċ��߂邩�͋��߂�ʐς̌`�ɂ���Ă��܂��g��������K�v������܂��B�����������Ƃ�O��ɁA���Ɏ������}�`�̖ʐς��d�ϕ��̎����g���ċ��߂Ă݂܂��傤�B�܂����߂�ϕ��̈�...