２重積分例題
初めに（20210619）
当サイトを参考にしてサイト作成・運営している方へお願い
バックリンクをお願いいたします。
例題①
以下の図に示される２つの直線に囲まれた面積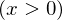
に対して重積分を使って求めてみましょう。
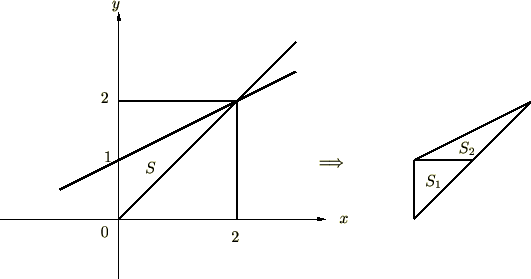
やり方としては、まず求める面積を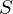
とし、それを上図右側のように２つに分割してそれぞれを
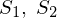と置きます。
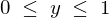の間では、
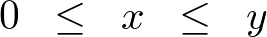
さらに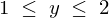
の間では、
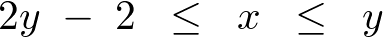
といった感じで積分領域を区分けし、これを計算していきます。
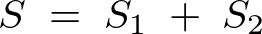
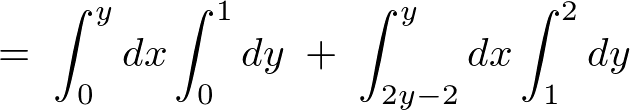
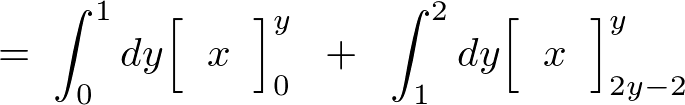
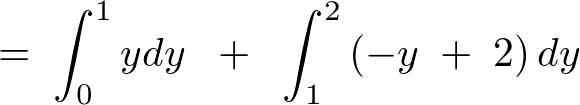
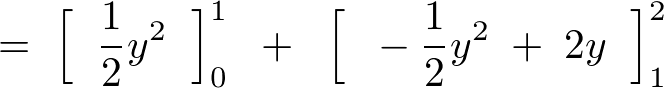
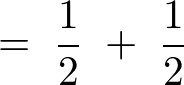
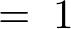
例題②
底辺の長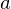さが
、高さが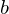
の二等辺三角形の面積。
３つの頂点の座標点を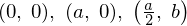
とします。
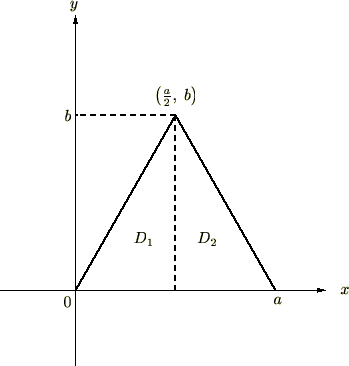
領域を図のように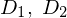
の二つに分けて考えます。
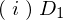の計算
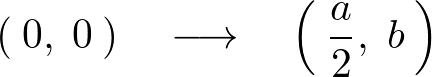
から、直線の方程式より、
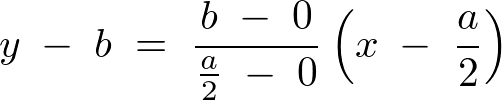
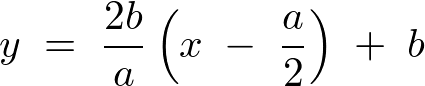
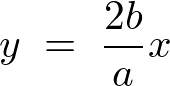
これが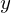
方向の上限になります。
以下のように積分領域を決定して計算していきます。
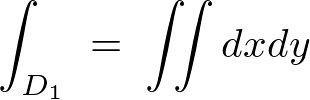
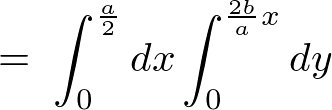
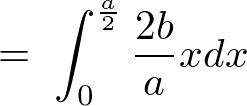
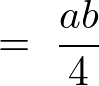
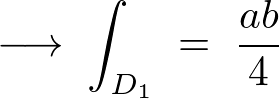
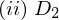の計算
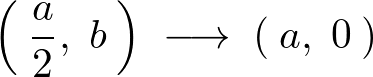
より、先ほどと同様にして直線の方程式に代入して計算していきます。
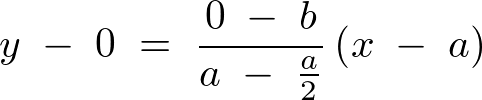
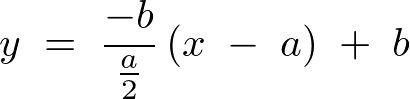
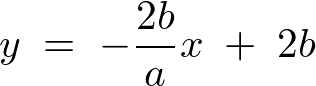
これが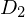
における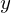方向の上限になります。
同様にして積分範囲を決定して計算していきます。
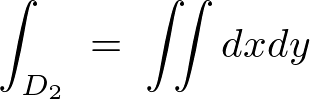
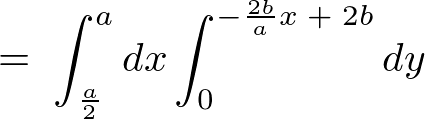
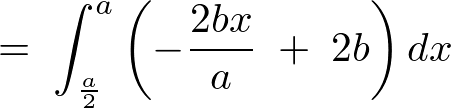
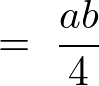
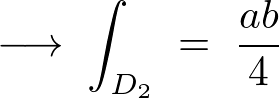
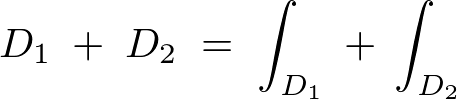
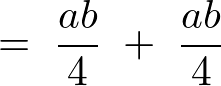
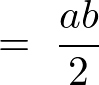
これより以下のように求まります。
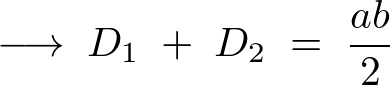
例題③
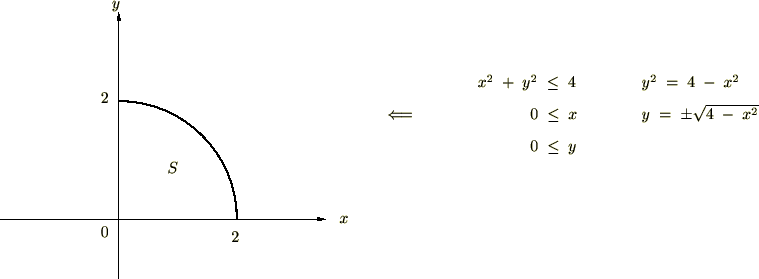
角度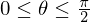
の範囲の半径が
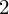の円の面積。
これの積分領域は、
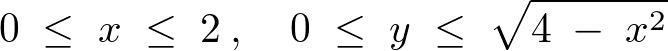
よって積分の式は次のようになります。
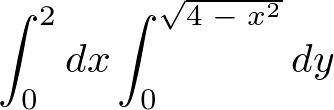
これを計算していきます。
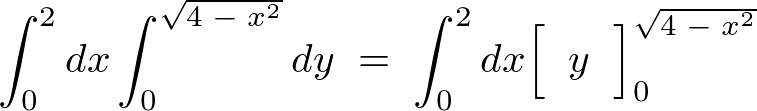
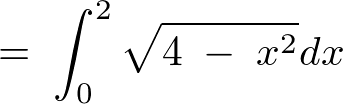
ここで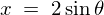
という変数変換（置換積分）をすると、
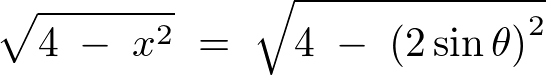
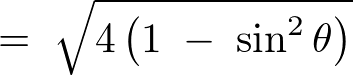
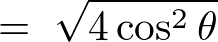
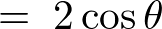
となるので、
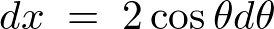
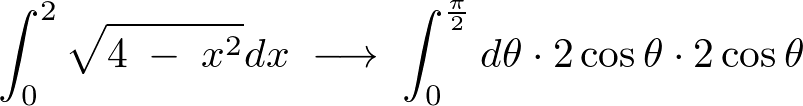
より、
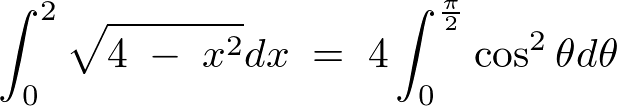
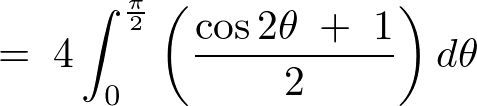
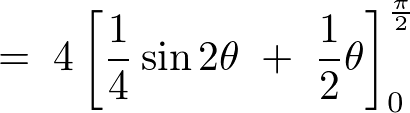
例題④
半径が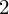の円の面積。
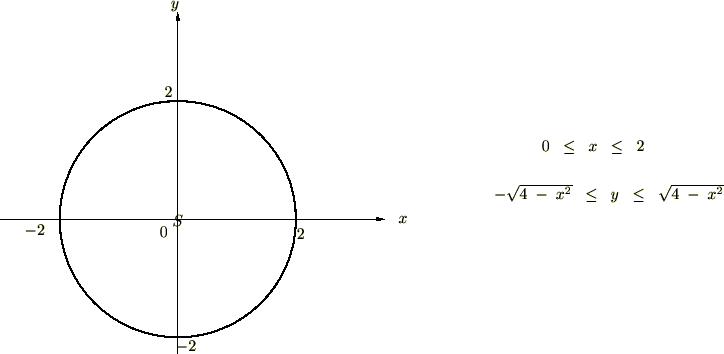
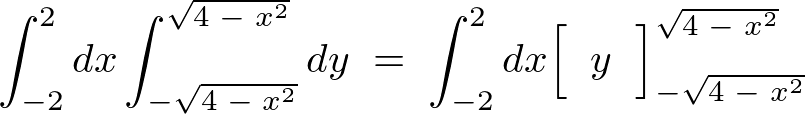
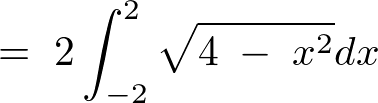
ここで先ほどと同じように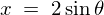とする変数変換をすると、
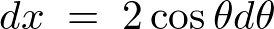
となるのでこれを代入して計算していけば、
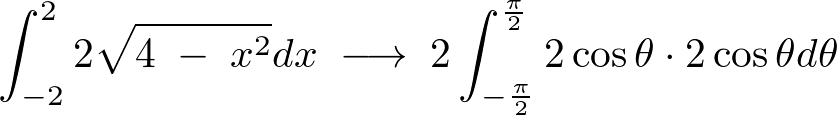
より、
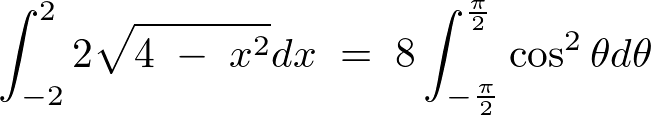
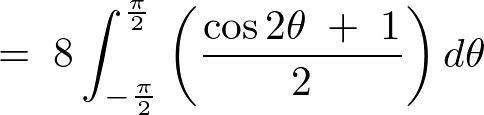
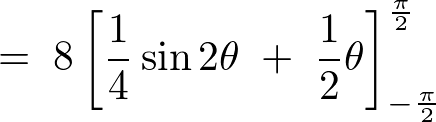
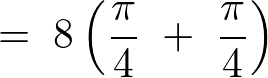
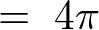
ついでに例題③と例題④の積分計算を今度は極座標でやってみましょう。
このデカルトから極座標へ移行する場合、
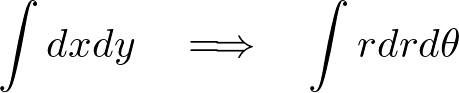
となることに注意します。
例題③極座標の場合
極座標のときの積分領域は、
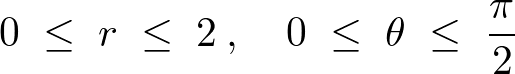
これにより、
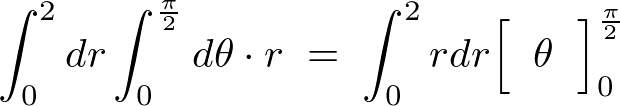
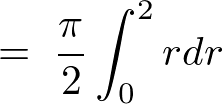
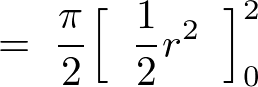
例題④極座標のとき
このときの積分領域は、
これにより、
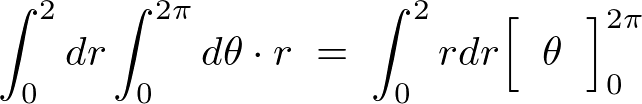
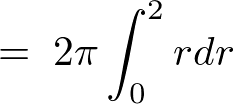
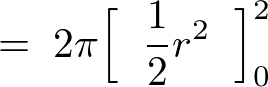
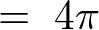
2重積分例題関連ページ
- 導関数
- 基本的に当サイトでは数学の苦手な方でも理解できることを目的としているので（証明のない数学などはありませんが）わかりづらい表記や説明はなるべく避け、あくまで道具としての数学を習得させることなどを目標としています。内容は慣性モーメントに関する部分だけでなく、最初のほうには慣性モーメントの計算において使用する微分積分に関する簡単な知識、二重積分および三重積分などの重積分法による面積および体積の導出などをこのカテゴリーに収めてあります。復習だとおもって軽く読み飛ばしてみてください。
- 偏微分
- 基本的に当サイトでは数学の苦手な方でも理解できることを目的としているので（証明のない数学などはありませんが）わかりづらい表記や説明はなるべく避け、あくまで道具としての数学を習得させることなどを目標としています。内容は慣性モーメントに関する部分だけでなく、最初のほうには慣性モーメントの計算において使用する微分積分に関する簡単な知識、二重積分および三重積分などの重積分法による面積および体積の導出などをこのカテゴリーに収めてあります。復習だとおもって軽く読み飛ばしてみてください。
- 一変数関数の積分
- 基本的に当サイトでは数学の苦手な方でも理解できることを目的としているので（証明のない数学などはありませんが）わかりづらい表記や説明はなるべく避け、あくまで道具としての数学を習得させることなどを目標としています。内容は慣性モーメントに関する部分だけでなく、最初のほうには慣性モーメントの計算において使用する微分積分に関する簡単な知識、二重積分および三重積分などの重積分法による面積および体積の導出などをこのカテゴリーに収めてあります。復習だとおもって軽く読み飛ばしてみてください。
- ２変数の積分－重積分
- 基本的に当サイトでは数学の苦手な方でも理解できることを目的としているので（証明のない数学などはありませんが）わかりづらい表記や説明はなるべく避け、あくまで道具としての数学を習得させることなどを目標としています。内容は慣性モーメントに関する部分だけでなく、最初のほうには慣性モーメントの計算において使用する微分積分に関する簡単な知識、二重積分および三重積分などの重積分法による面積および体積の導出などをこのカテゴリーに収めてあります。復習だとおもって軽く読み飛ばしてみてください。
- 2重積分
- 慣性モーメントとは、簡単に説明すれば物体（剛体）の回転のしづらさ、回りだす変化のしにくさを示す物体の物理的な特性のことだと考えることができるでしょう。またさらに別の言い方をすれば回転の方程式といえるかもしれません。このサイトは主にこの慣性モーメントの導出の仕方と計算法を中心に解説した内容になっています。
