2�d�ϕ�
���߂Ɂi20210619�j
���T�C�g���Q�l�ɂ��ăT�C�g�y�ѓ���(youtube)�쐬�E�^�c���Ă�����ւ̂��肢
�y�Љ�l�Ƃ��čŒ���̃��[���A�}�i�[�͎��܂��傤�z
�ߔN�A���h���C���R���e���c�̖��炩�ȓ��p�Ǝv����T�C�g�E���悪�ꕔ�U������܂��B
�Q�l�ɂ����̂ł���ΏЉ���N�Ȃǂ̒��߂�����Ƃ������Ή��͕K�����肢�������܂��B
�d�ϕ��|�l�����Ƃ��̎菇
�ϕ��̎�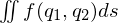 �ɂ����Ă̔����ʐϗv�f
�ɂ����Ă̔����ʐϗv�f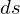 �͑S�Z�N�V�����ɂ����Ď����ꂽ�ɍ��W�ƃf�J���g�̂Q��ނ��������A�ǂ�����g���ċ��߂邩�͋��߂�ʐς̌`�ɂ���Ă��܂��g��������K�v������܂��B
�͑S�Z�N�V�����ɂ����Ď����ꂽ�ɍ��W�ƃf�J���g�̂Q��ނ��������A�ǂ�����g���ċ��߂邩�͋��߂�ʐς̌`�ɂ���Ă��܂��g��������K�v������܂��B
�����������Ƃ�O��ɁA���Ɏ������}�`�̖ʐς��d�ϕ��̎����g���ċ��߂Ă݂܂��傤�B
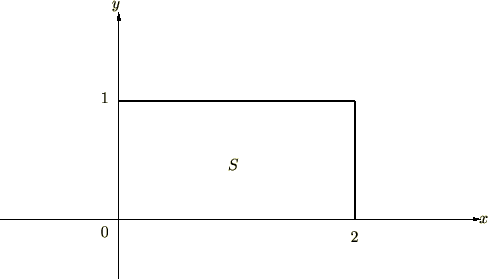
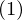 �܂����߂�ϕ��̈�
�܂����߂�ϕ��̈�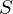 ��
��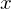 ��
��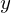 �̕s�����ŏ����\���܂��B
�̕s�����ŏ����\���܂��B
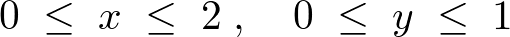
����ɂ��A
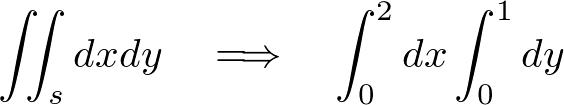
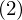 �ϕ��̎��s�c��̕������ϕ������s���܂��B
�ϕ��̎��s�c��̕������ϕ������s���܂��B
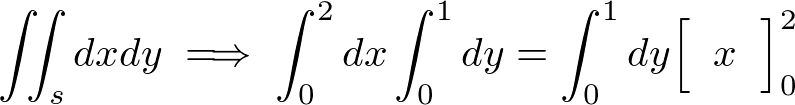
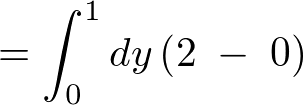
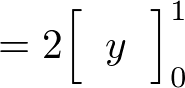
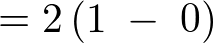
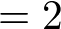
���x�͎��̐}�`�ɑ��ĂQ�d�ϕ������s���Ă݂܂��傤�B
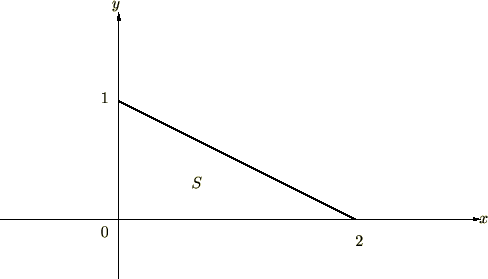
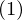 �ŏ��ɐϕ��̈�����߂܂����A�����Ő�قǂ̂�����͕킷��A
�ŏ��ɐϕ��̈�����߂܂����A�����Ő�قǂ̂�����͕킷��A
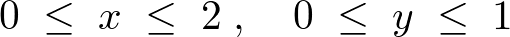
�Ƃ������Ȃ�܂�������͊ԈႢ�ŁA�����������}�`�̏ꍇ�A�܂��Q�̕ϐ��̂����̂P����������ɓ������Ƃ�����Ƃ����܂��B
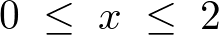
���̂悤�ɂ����玟�ɂ�����̕ϐ�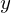 �̐������l���܂��B
�̐������l���܂��B
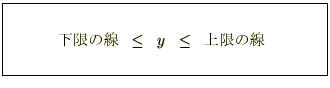
�����ɂ�����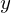 �̒l��
�̒l��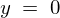 �A
�A
����ɂ�����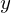 �̒l��
�̒l��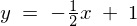 �B
�B
����ɂ��A
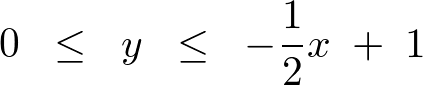
�ƂȂ�܂��B
���������āA
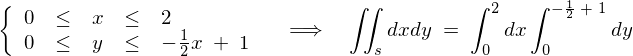
�Ƃ������`�ɂȂ�܂��B
�����������}�`�ɑ��Ă̏d�ϕ��͑������ӂ��K�v�ł��B
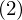 �ϕ��̎��s�B
�ϕ��̎��s�B
�����̂Ƃ��ɂ�����ϕ������͐ϕ��̈�̒��ɑ��̕ϐ����܂�ł�����̂����Ɏ��s����悤�ɂ��Ă��������B
�Ȃ̂ł��̐ϕ��v�Z�ɂ����Ă͂܂�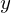 ����ɂȂ�܂��B
����ɂȂ�܂��B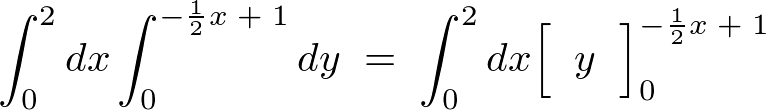
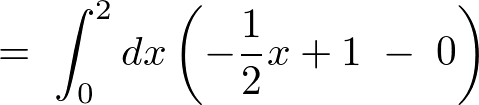
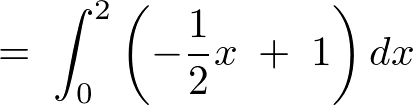
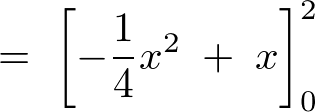
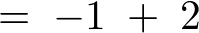
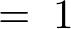
�������ɒu���č��x�͍ŏ���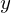 �������ꍇ������Ă݂�Ɛϕ��̈�́A
�������ꍇ������Ă݂�Ɛϕ��̈�́A

�ƂȂ�܂��B
���ۂɌv�Z���Ă݂�ƁA
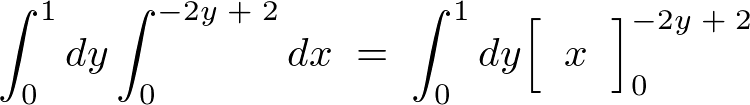
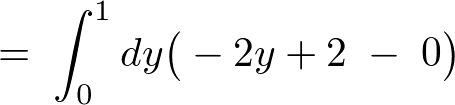
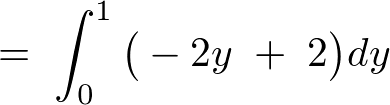
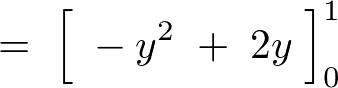
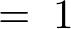
2�d�ϕ��֘A�y�[�W
- ����
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B
- ����
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B
- ��ϐ����̐ϕ�
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B
- �Q�ϐ��̐ϕ��|�d�ϕ�
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B
- 2�d�ϕ����
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B





















