�Q�ϐ��̐ϕ��|�d�ϕ�
���߂Ɂi20210619�j
���T�C�g���Q�l�ɂ��ăT�C�g�y�ѓ���(youtube)�쐬�E�^�c���Ă�����ւ̂��肢
�y�Љ�l�Ƃ��čŒ���̃��[���A�}�i�[�͎��܂��傤�z
�ߔN�A���h���C���R���e���c�̖��炩�ȓ��p�Ǝv����T�C�g�E���悪�ꕔ�U������܂��B
�Q�l�ɂ����̂ł���ΏЉ���N�Ȃǂ̒��߂�����Ƃ������Ή��͕K�����肢�������܂��B
�`�Ƃ��Ă͎��̂悤�ɂȂ�܂��B
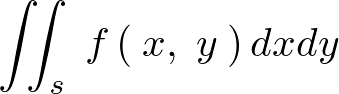
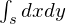 �̈Ӗ�
�̈Ӗ�

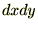 ��
�� ���W�n�ŕ\�������Ƃ��̔����ʐςɂȂ�܂��B
���W�n�ŕ\�������Ƃ��̔����ʐςɂȂ�܂��B
���������̔����ʐς͍��W�n�ɂ���ĈقȂ�܂��B
���W�n�Ɉˑ����Ȃ��`�ł�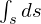 �Ə����A��قǂ̃f�J���g�\���ɂ����Ă�
�Ə����A��قǂ̃f�J���g�\���ɂ����Ă�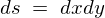 �ł��B
�ł��B
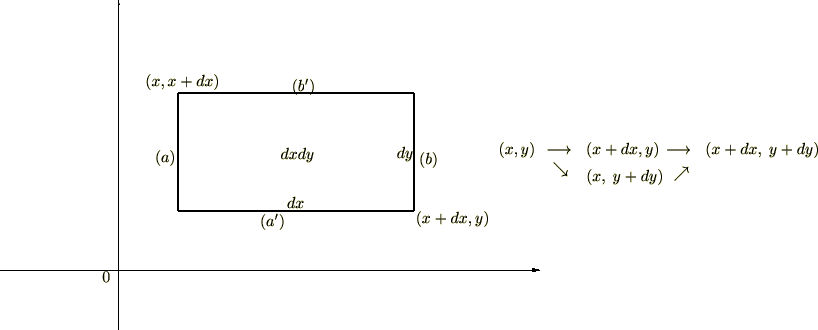
�����ł���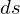 ��}�ōl���Ă݂܂��傤�B
��}�ōl���Ă݂܂��傤�B
���W�n��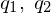 �̂Ƃ��A
�̂Ƃ��A
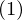 �@�_
�@�_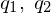 ���l����B
���l����B
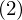 ���ׂĂ̕ϐ���
���ׂĂ̕ϐ���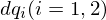 ���炷�B
���炷�B
���̎����ׂĂ̂��炵�����l���܂��B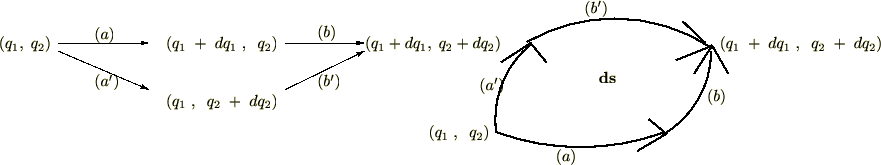
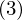 ���ׂĂ̌o�H�ɂ���Ĉ͂܂ꂽ�����̖ʐς��ʐϗv�f
���ׂĂ̌o�H�ɂ���Ĉ͂܂ꂽ�����̖ʐς��ʐϗv�f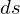 �ɂȂ�܂��B
�ɂȂ�܂��B
- �f�J���g�ł�
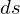
- �ɍ��W�ł�
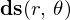
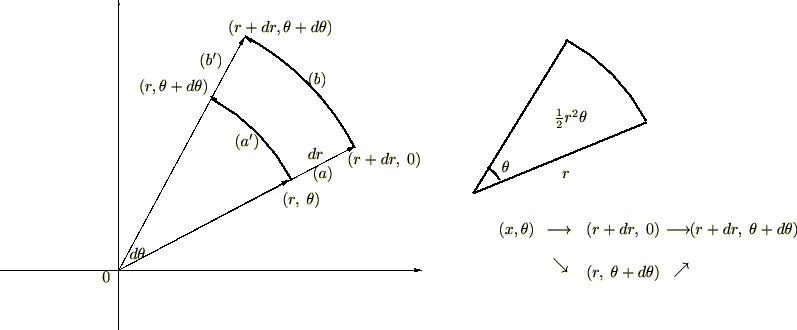
�ɍ��W�ɂ���������ʐ�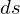 �̋��ߕ�
�̋��ߕ�
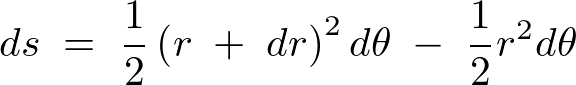
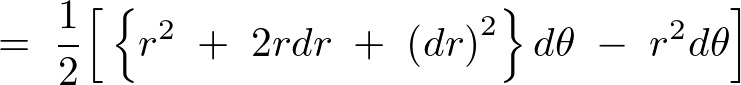
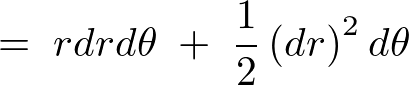
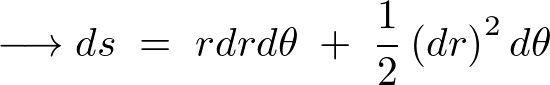
���߂�ꂽ��L�̎��ɂ����āA��ꍀ�������ʂ̂Q���A��������ʂ̂R���ɂȂ�܂��B
�Ƃ肠�����A���̏�ʂɂ����Ă͏�L�̔����ʂ̂R���̓L�����Z���ł���Ƃ��܂��傤�B��������Ƌɍ��W�ɂ���������ʐ�
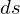 �͎��̂悤�ɕ\���ł��邱�ƂɂȂ�܂��B
�͎��̂悤�ɕ\���ł��邱�ƂɂȂ�܂��B
�d�ϕ��֘A�y�[�W
- ����
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B
- ����
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B
- ��ϐ����̐ϕ�
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B
- 2�d�ϕ�
- �������[�����g�Ƃ́A�ȒP�ɐ�������Ε��́i���́j�̉�]�̂��Â炳�A��肾���ω��̂��ɂ������������̂̕����I�ȓ����̂��Ƃ��ƍl���邱�Ƃ��ł���ł��傤�B�܂�����ɕʂ̌�����������Ή�]�̕������Ƃ����邩������܂���B���̃T�C�g�͎�ɂ��̊������[�����g�̓��o�̎d���ƌv�Z�@�𒆐S�ɉ���������e�ɂȂ��Ă��܂��B
- 2�d�ϕ����
- ��{�I�ɓ��T�C�g�ł͐��w�̋��ȕ��ł������ł��邱�Ƃ�ړI�Ƃ��Ă���̂Łi�ؖ��̂Ȃ����w�Ȃǂ͂���܂��j�킩��Â炢�\�L������͂Ȃ�ׂ������A�����܂œ���Ƃ��Ă̐��w���K�������邱�ƂȂǂ�ڕW�Ƃ��Ă��܂��B���e�͊������[�����g�Ɋւ��镔�������łȂ��A�ŏ��̂ق��ɂ͊������[�����g�̌v�Z�ɂ����Ďg�p��������ϕ��Ɋւ���ȒP�Ȓm���A��d�ϕ�����юO�d�ϕ��Ȃǂ̏d�ϕ��@�ɂ��ʐς���ё̐ς̓��o�Ȃǂ����̃J�e�S���[�Ɏ��߂Ă���܂��B���K���Ƃ������Čy���ǂݔ���Ă݂Ă��������B





















