�����ʐϗv�fdv�̋��ߕ�
���߂Ɂi20210619�j
���T�C�g���Q�l�ɂ��ăT�C�g�y�ѓ���(youtube)�쐬�E�^�c���Ă�����ւ̂��肢
�y�Љ�l�Ƃ��čŒ���̃��[���A�}�i�[�͎��܂��傤�z
�ߔN�A���h���C���R���e���c�̖��炩�ȓ��p�Ǝv����T�C�g�E���悪�ꕔ�U������܂��B
�Q�l�ɂ����̂ł���ΏЉ���N�Ȃǂ̒��߂�����Ƃ������Ή��͕K�����肢�������܂��B
dv�v�Z�@-���R�r�A�����g������
���W�n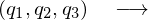 �@�@�@���W�n
�@�@�@���W�n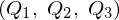 �֍��W�ϊ�����Ƃ���قǂ̃Z�N�V�����ŏo�Ă������s�������Ǝ��̂悤�ɂȂ�܂��B
�֍��W�ϊ�����Ƃ���قǂ̃Z�N�V�����ŏo�Ă������s�������Ǝ��̂悤�ɂȂ�܂��B
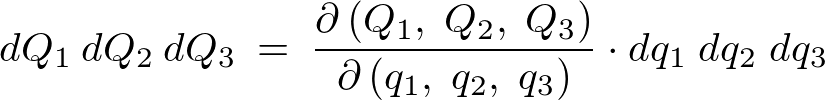
�����Œ��������̍s��́A
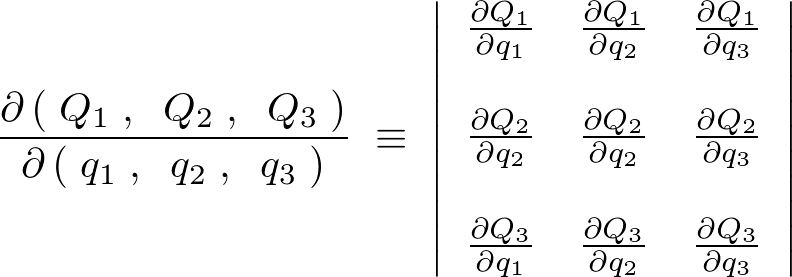
�ƂȂ邱�Ƃɒ������܂��B
�ɍ��W
���ۂɃf�J���g����ɂֈڍs����Ƃ���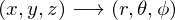 �����s�ŋ��߂Ă݂܂��傤�B
�����s�ŋ��߂Ă݂܂��傤�B
�܂��A
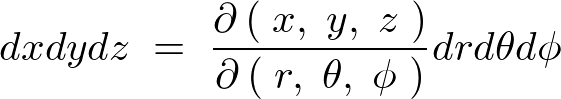
���A����ɑ�����s�i���R�r�A���j�͎��̂悤�ɂȂ�܂��B
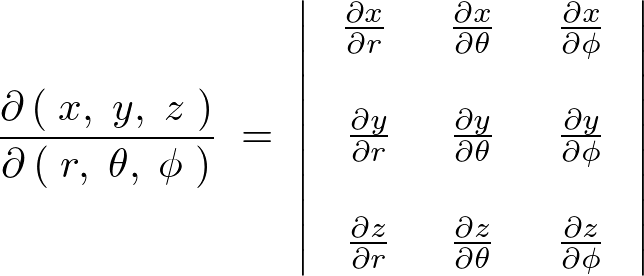
���̊��s�i���R�r�A���j�ɂ�����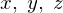 �̈ʒu�\���ɑ��Ă͂��̂��̂��g���܂��B
�̈ʒu�\���ɑ��Ă͂��̂��̂��g���܂��B
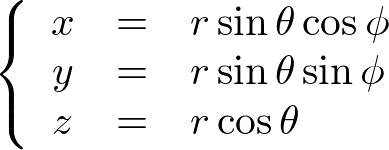
���������R�r�A���̍s�̒��Ɏ�����邻�ꂼ��̕Δ����̎��ɓ��Ă͂߂Čv�Z���Ă����A
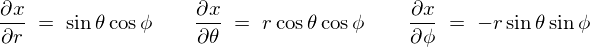
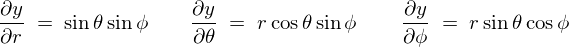
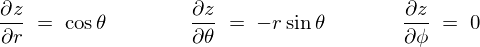
��L�̌��ʂɂ��ɂ��ɍ��W�ɂ����郄�R�r�A���́A
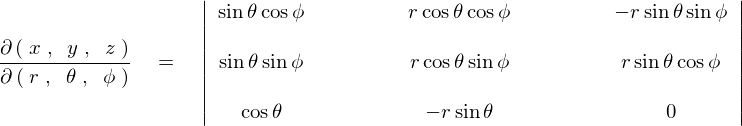
�ƂȂ�̂ŁA���x�͎��ۂɂ��̃��R�r�A�����v�Z���Ă����܂��B
���Ȃ݂ɂ����ł̓T���X�ɂ��v�Z�@�ł͂Ȃ��A�s�W�J�@�Ƃ��������ł��̌v�Z�ߒ��������܂��B
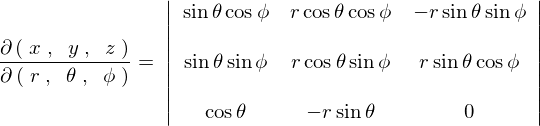
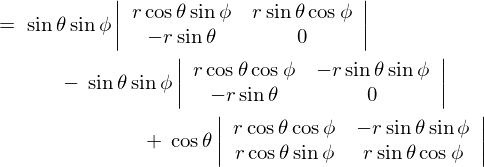
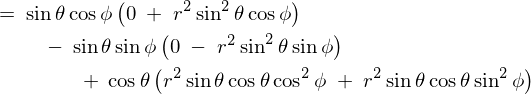
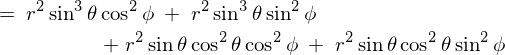
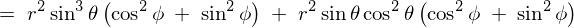
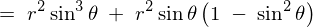
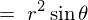
����ċɍ��W�ɂ���������̐ϗv�f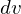 �͎��̂悤�ɂȂ�܂��B
�͎��̂悤�ɂȂ�܂��B
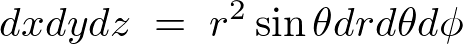
�~�����W
���x�̓f�J���g����~�����W�ւ̃��R�r�A�������߂Ă݂܂��傤�B
�~�����W�́A
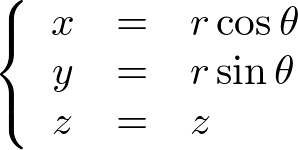
�ƂȂ�̂ŁA���̉~�����W�ɑ��郄�R�r�A���̒��̕Δ����̎��́A
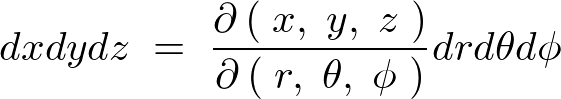
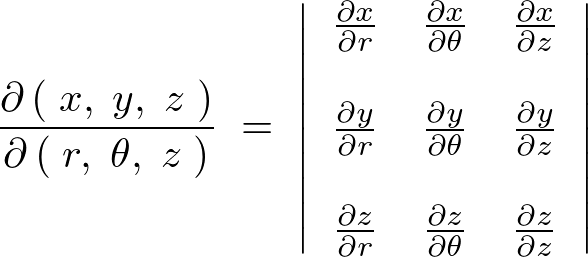
���ꂼ��̕Δ������v�Z���Ă����ƁA
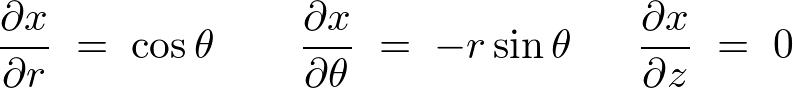
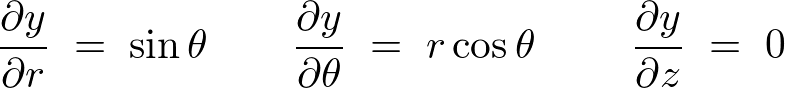
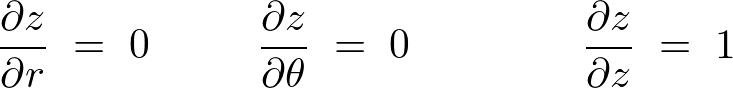
������Ă����܂��B
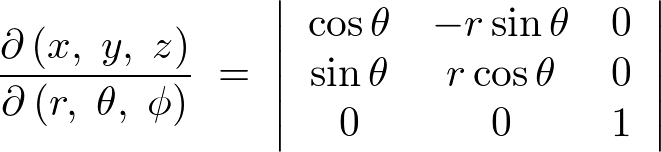
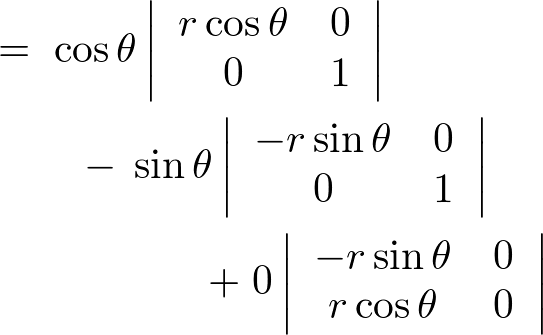
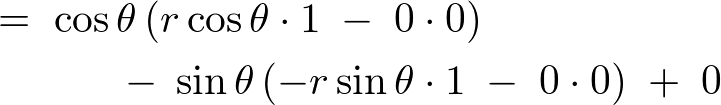
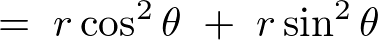
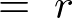
����ĉ~�����W�ɂ���������̐ϗv�f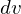 �͎��̂悤�ɂȂ�܂��B
�͎��̂悤�ɂȂ�܂��B
dv�̌v�Z�@�|���R�r�A�����g�������֘A�y�[�W
- �ϐ��ϊ��ƃ��R�r�A��(�쐬��)
- ������W�n�𑼂̍��W�n�֕ϊ�����Ƃ��Ɋ��s�������̂�p���܂��B���̎��̊��s�����R�r�A���ƌĂт܂��B�����ł͂��̃��R�r�A���Ɋւ��Ă��̈Ӗ����l�@���Ă����܂��B
- �����ʐϗv�f�̌v�Z
- ������W�n�𑼂̍��W�n�֕ϊ�����Ƃ��Ɋ��s�������̂�p���܂��B���̎��̊��s�����R�r�A���ƌĂт܂��B���̃��R�r�A�����g���Ď��ۂɃf�J���g���W�n����ɍ��W�A����ɂ͉~�����W�n�ւ̕ϊ����A�Δ�����s��v�Z���s���ċ��߂܂��B
- �����v�Z�̖��
- ������W�n�𑼂̍��W�n�֕ϊ�����Ƃ��Ɋ��s�������̂�p���܂��B���̎��̊��s�����R�r�A���ƌĂт܂��B���̃��R�r�A�����g���Ď��ۂɃf�J���g���W�n����ɍ��W�A����ɂ͉~�����W�n�ւ̕ϊ����A�Δ�����s��v�Z���s���ċ��߂܂��B
- ����
- ������W�n�𑼂̍��W�n�֕ϊ�����Ƃ��Ɋ��s�������̂�p���܂��B���̎��̊��s�����R�r�A���ƌĂт܂��B���̃��R�r�A�����g���Ď��ۂɃf�J���g���W�n����ɍ��W�A����ɂ͉~�����W�n�ւ̕ϊ����A�Δ�����s��v�Z���s���ċ��߂܂��B





















