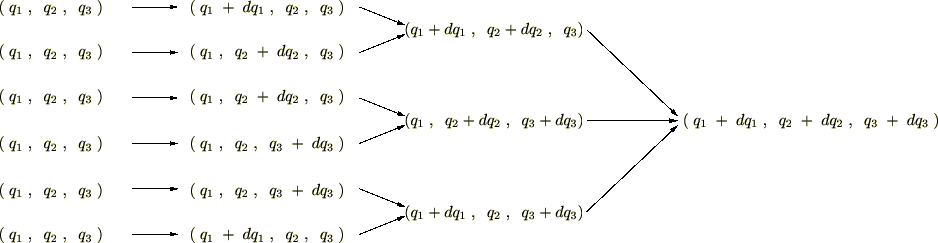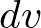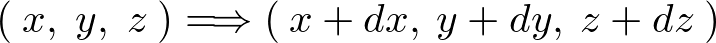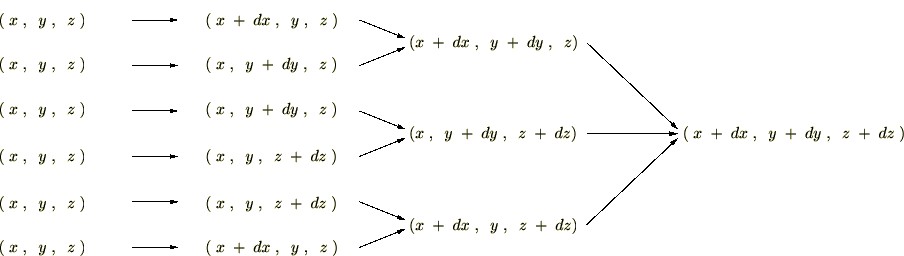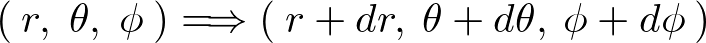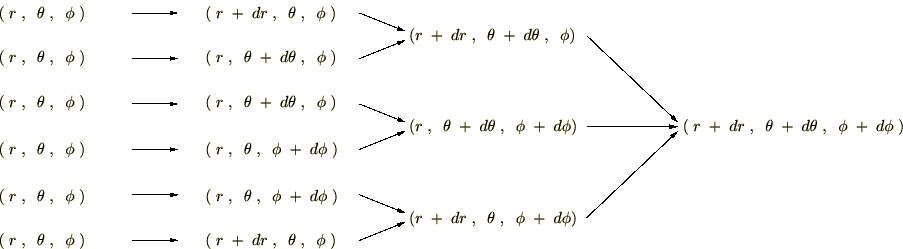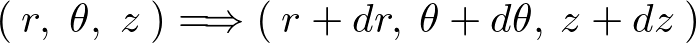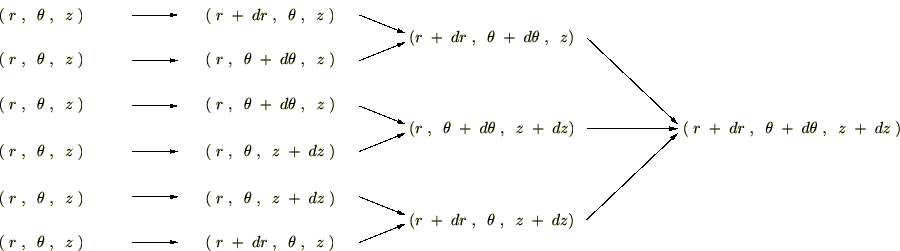�����ʐϗv�f�̌v�Z
���߂Ɂi20210619�j
���T�C�g���Q�l�ɂ��ăT�C�g�y�ѓ���(youtube)�쐬�E�^�c���Ă�����ւ̂��肢
�y�Љ�l�Ƃ��čŒ���̃��[���A�}�i�[�͎��܂��傤�z
�ߔN�A���h���C���R���e���c�̖��炩�ȓ��p�Ǝv����T�C�g�E���悪�ꕔ�U������܂��B
�Q�l�ɂ����̂ł���ΏЉ���N�Ȃǂ̒��߂�����Ƃ������Ή��͕K�����肢�������܂��B
���s�i���R�r�A���j
������W�n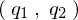 �𑼂̍��W�n
�𑼂̍��W�n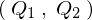 �֕ς���Ƃ��A
�֕ς���Ƃ��A
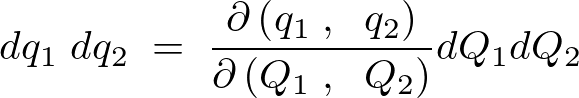
�Ƃ����������藧���܂��B
���̂Ƃ��� �����R�r�A���i���s�j�ƌĂсA���̂悤�ɕ\������̂ɂȂ�܂��B
�����R�r�A���i���s�j�ƌĂсA���̂悤�ɕ\������̂ɂȂ�܂��B
���ۂɃf�J���g����ɍ��W�ւ̕ϊ������̃��R�r�A���i���s�j�������ċ��߂Ă݂܂��傤�B
�܂��A�f�J���g���W�ɂ����� ��\���ƁA
��\���ƁA
����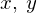 �̎������ꂼ��
�̎������ꂼ��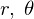 �ɂ���ĕΔ������Ă����܂��B
�ɂ���ĕΔ������Ă����܂��B
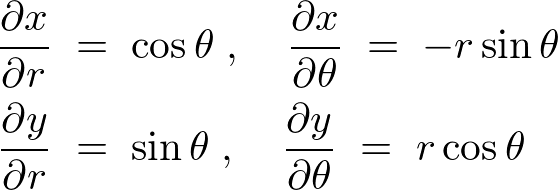
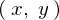 ���W�n����
���W�n����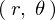 �ֈڍs���郄�R�r�A���́A
�ֈڍs���郄�R�r�A���́A
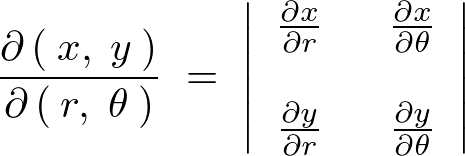
����ɂ��ꂼ��������Ă��̍s���v�Z���Ă����܂��B
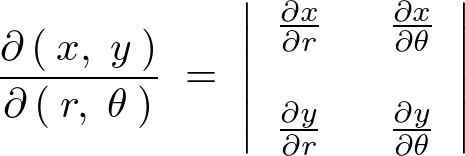
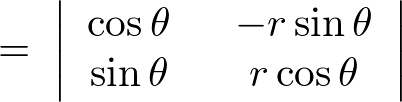
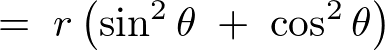
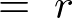
���j20220727�����B�E�ӑ�2���̍s��2�s2���rcos�Ƃ�cos�ƂɂȂ��Ă��܂����B���������l�ѐ\���グ�܂��B
��L�̌v�Z���ʂ�����A
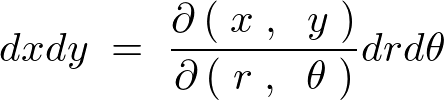
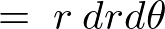
����ăf�J���g���W��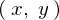 �́A���R�r�A���ɂ�镽�ʋɍ��W�ϊ��ɂ���Ĉȉ��̂悤�ɋ��܂�܂��B
�́A���R�r�A���ɂ�镽�ʋɍ��W�ϊ��ɂ���Ĉȉ��̂悤�ɋ��܂�܂��B
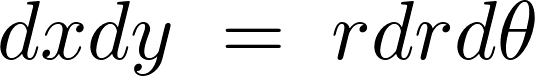
�����̐ϗv�f�̈ړ����[�g
��ʓI�ȍ��W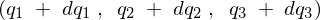 �ւ̈ړ����l���Ă݂܂��傤�B
�ւ̈ړ����l���Ă݂܂��傤�B
���̈ړ����[�g�ɂ�
 �ʂ肪����܂��B
�ʂ肪����܂��B
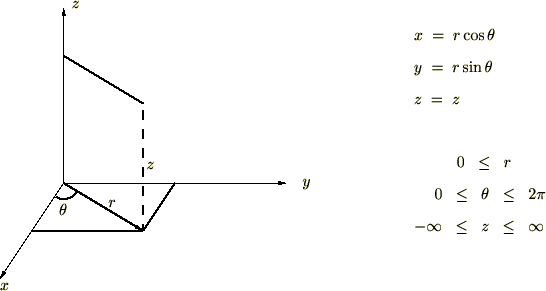
�ɍ��W�n
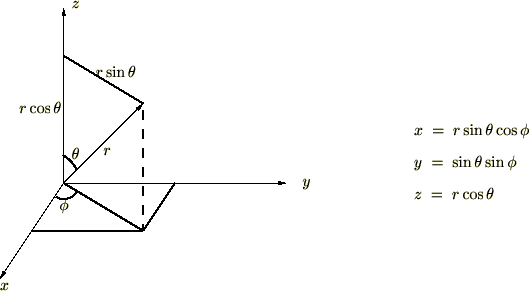
�����ʐϗv�f�̌v�Z�֘A�y�[�W
- �ϐ��ϊ��ƃ��R�r�A��(�쐬��)
- ������W�n�𑼂̍��W�n�֕ϊ�����Ƃ��Ɋ��s�������̂�p���܂��B���̎��̊��s�����R�r�A���ƌĂт܂��B�����ł͂��̃��R�r�A���Ɋւ��Ă��̈Ӗ����l�@���Ă����܂��B
- dv�̌v�Z�@
- �������[�����g�Ƃ́A�ȒP�ɐ�������Ε��́i���́j�̉�]�̂��Â炳�A��肾���ω��̂��ɂ������������̂̕����I�ȓ����̂��Ƃ��ƍl���邱�Ƃ��ł���ł��傤�B�܂�����ɕʂ̌�����������Ή�]�̕������Ƃ����邩������܂���B���̃T�C�g�͎�ɂ��̊������[�����g�̓��o�̎d���ƌv�Z�@�𒆐S�ɉ���������e�ɂȂ��Ă��܂��B
- �����v�Z�̖��
- ������W�n�𑼂̍��W�n�֕ϊ�����Ƃ��Ɋ��s�������̂�p���܂��B���̎��̊��s�����R�r�A���ƌĂт܂��B���̃��R�r�A�����g���Ď��ۂɃf�J���g���W�n����ɍ��W�A����ɂ͉~�����W�n�ւ̕ϊ����A�Δ�����s��v�Z���s���ċ��߂܂��B
- ����
- ������W�n�𑼂̍��W�n�֕ϊ�����Ƃ��Ɋ��s�������̂�p���܂��B���̎��̊��s�����R�r�A���ƌĂт܂��B���̃��R�r�A�����g���Ď��ۂɃf�J���g���W�n����ɍ��W�A����ɂ͉~�����W�n�ւ̕ϊ����A�Δ�����s��v�Z���s���ċ��߂܂��B