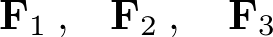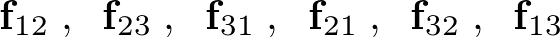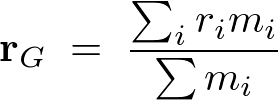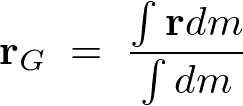���_�n�̗͊w
���߂Ɂi20210619�j
���T�C�g���Q�l�ɂ��ăT�C�g�y�ѓ���(youtube)�쐬�E�^�c���Ă�����ւ̂��肢
�y�Љ�l�Ƃ��čŒ���̃��[���A�}�i�[�͎��܂��傤�z
�ߔN�A���h���C���R���e���c�̖��炩�ȓ��p�Ǝv����T�C�g�E���悪�ꕔ�U������܂��B
�Q�l�ɂ����̂ł���ΏЉ���N�Ȃǂ̒��߂�����Ƃ������Ή��͕K�����肢�������܂��B
�������̎��_����Ȃ镨���n�̘b
���U�I�Ȍn
���Ɏ������O���_�n���l���܂��B
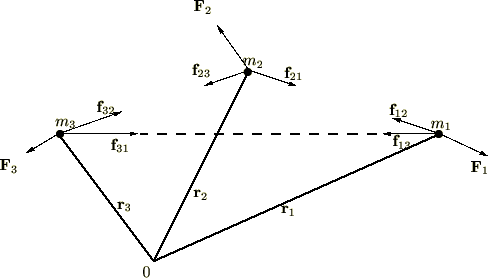
���̎��e���_�ɓ����͂́A
| �O�� |
|
|---|---|
| ���� |
|
����ɓ��O�̏ꍇ�A�K����p�E����p�̖@���ɂ���đ傫���������Ō������t�̈�g�̗͂�����ƍl���܂��B
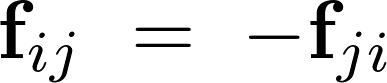
�����@��
��L�̎O���_�n�ɂ��Ă͎��̂悤�ȉ^�����������������܂��B
�P�`�R�̎��_�̉^���������́A���ꂼ��A
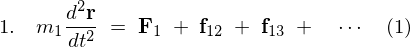
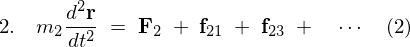
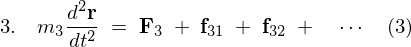
����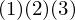 �����ꂼ��݂����ƁA
�����ꂼ��݂����ƁA
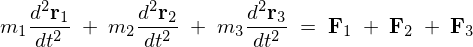
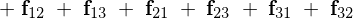
�ƂȂ�܂����A�����Ő�قǎ�������p����p�̂ɂ���g�̗�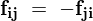 ���g���ƁA
���g���ƁA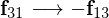 �ȂǂƂȂ�̂Ō��ǁA
�ȂǂƂȂ�̂Ō��ǁA
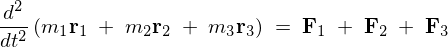
�Ƃ�������ɂȂ�܂��B
����ɂ����ɂ����ďd�S���A
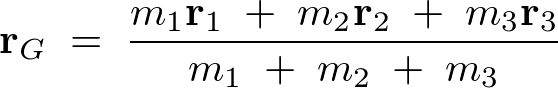
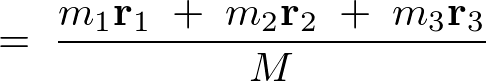
�Ƃ����ꍇ�A���̂悤�ɕ\���ł��܂��B
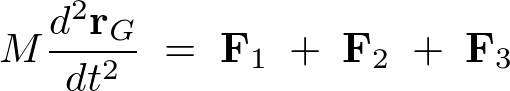
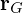 �̂Ƃ���Ɏ���
�̂Ƃ���Ɏ���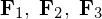 �̎��_�������Ă����
�̎��_�������Ă����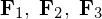 �i���ׂĂ̊O�́j�������Ă���\�B
�i���ׂĂ̊O�́j�������Ă���\�B
���Ȃ��G�c�Ȍ������ɂȂ�܂���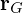 �͎��̂悤�ȋ敪�����ł��邩�Ǝv���܂��B
�͎��̂悤�ȋ敪�����ł��邩�Ǝv���܂��B
| ���U�I�Ȍn |
|
|---|---|
| �A���I�Ȍn |
|
���@�@�|�@�_�̏d�S
�ȉ��Ɏ����悤�Ȓ�����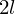 �̋ψ�Ȏ���
�̋ψ�Ȏ���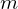 �̖_�̏d�S�����߂Ă݂܂��傤�B
�̖_�̏d�S�����߂Ă݂܂��傤�B
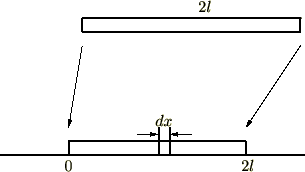
�܂�������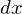 �̕����̎���
�̕����̎���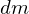 �����߂܂��B
�����߂܂��B
�f�B�����W�����P�Ƒ�����A���̖_�̐����x�́A
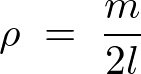
����ɂ��A
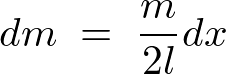
�A���I�ł���̂ŁA
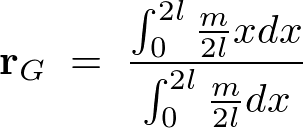
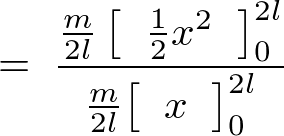
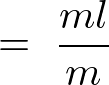
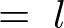
����Ē���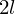 �̖_�̏d�S�͈ȉ��̂悤�ɂȂ�܂��B
�̖_�̏d�S�͈ȉ��̂悤�ɂȂ�܂��B
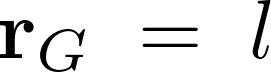
���A�@�|�@�~���̏d�S
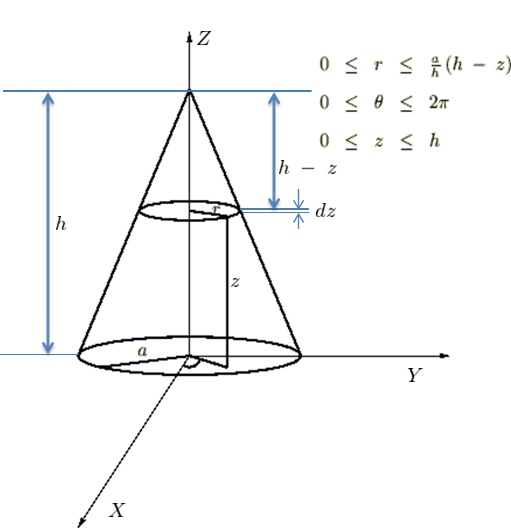
��}�̂悤�ȋψ�Ȏ��ʂ�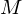 �ō�����
�ō�����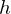 �A��ʂ̔��a��
�A��ʂ̔��a��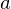 �̉~���̏d�S�����߂Ă݂܂��傤�B
�̉~���̏d�S�����߂Ă݂܂��傤�B
�܂����~���̑̐��́A
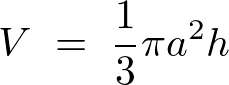
����ɂ��~���̑̐ϖ��x�́A
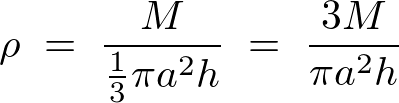
�����ł͉~���̔C�ӂ̍����ɑ��锼�a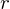 �Ŗʐς�
�Ŗʐς�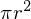 �A����
�A����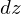 �̔��������̉~�Ղ̎��ʂ�
�̔��������̉~�Ղ̎��ʂ�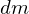 �Ƃ���ƁA
�Ƃ���ƁA
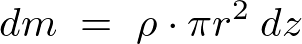
�Ƃ��āA���̂悤�ɉ~���̎��ʂ�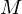 �ƒu���܂��B
�ƒu���܂��B
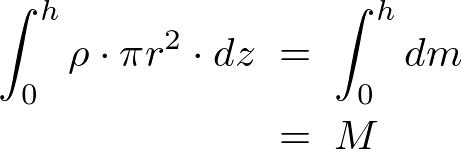
�܂��A�~���̏d�S�Ɋւ��Ă͐}����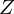 ������ɂ���ƍl������̂Ŏ���
������ɂ���ƍl������̂Ŏ���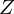 ����̔C�ӂ̓_z�������ϐ��Ƃ��Ď��̂悤�ɍ̗p���܂��B
����̔C�ӂ̓_z�������ϐ��Ƃ��Ď��̂悤�ɍ̗p���܂��B
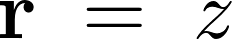
������������A
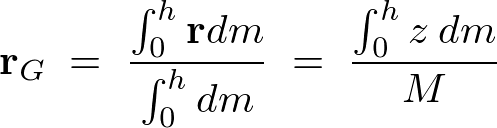
�܂��A�}����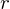 �Ɋւ��Ă͈ȉ��̂悤�ȑ����W���g���ē����Ă��܂��B
�Ɋւ��Ă͈ȉ��̂悤�ȑ����W���g���ē����Ă��܂��B
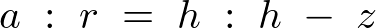
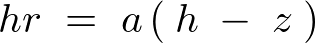
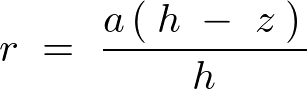
�����ɂ��A�~���̏d�S�͕���̉~�����ʂ�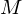 �Ƃ킩���Ă���̂ŏ�L���̕��q���킩��Ώd�S�̈ʒu�����܂邱�ƂɂȂ�܂��B
�Ƃ킩���Ă���̂ŏ�L���̕��q���킩��Ώd�S�̈ʒu�����܂邱�ƂɂȂ�܂��B
��L���̕��q�̕������v�Z���Ă����܂��B
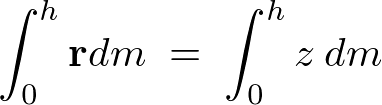
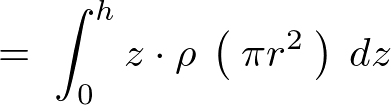
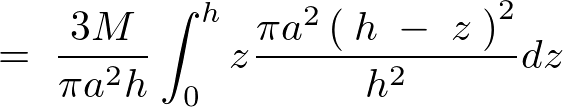
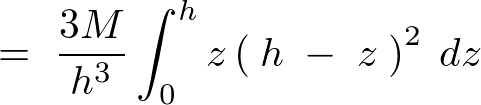
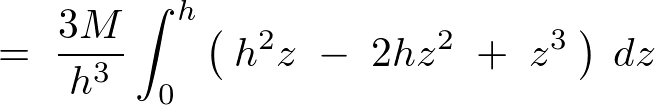
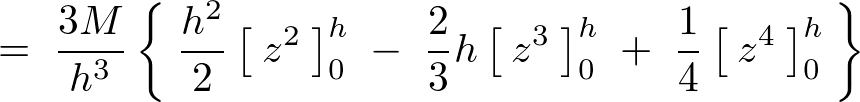
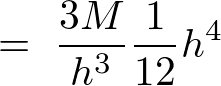
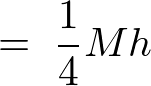
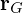 �̎��ɑ�����Ă����܂��B
�̎��ɑ�����Ă����܂��B
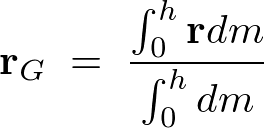
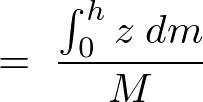
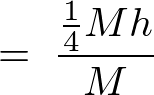
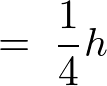
������A�~���̏d�S�͈ȉ��̂悤�ɋ��܂�܂��B
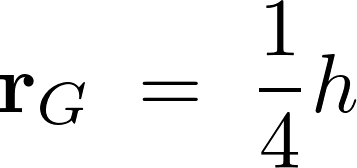
���B�@�|�@�����`�̏d�S
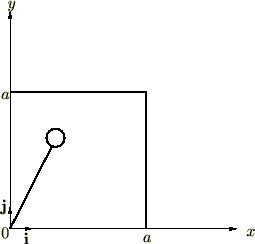
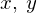 ���ɂ����邻�ꂼ��̒P�ʃx�N�^�[��
���ɂ����邻�ꂼ��̒P�ʃx�N�^�[��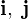 �Ƃ���ƁA
�Ƃ���ƁA
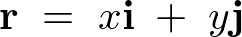
�ƂȂ�̂ŁA
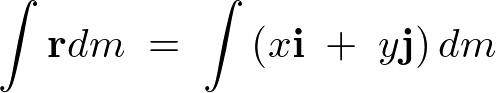
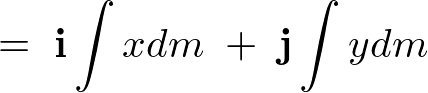
���������̖ʐς�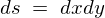 �A
�A
���x�́A
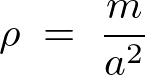
�����ɂ��A
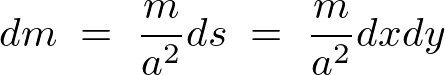
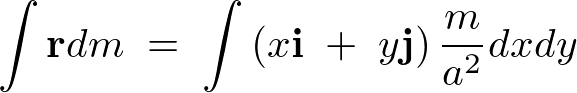
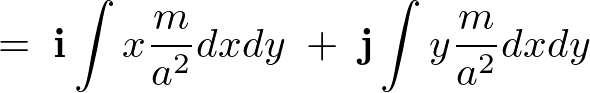
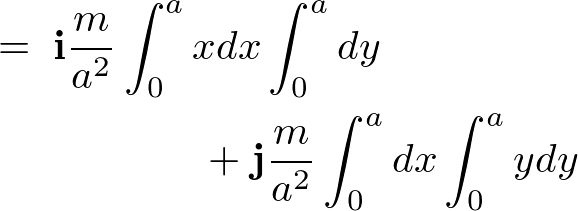
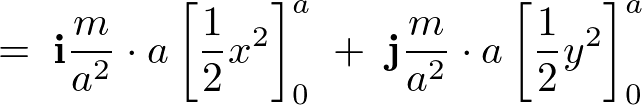
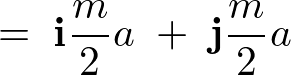
����Đ����`�̔̏d�S�́A
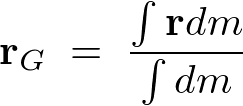
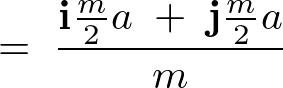
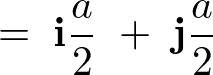
����Ĉȉ��̂悤�ɋ��܂�܂��B
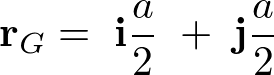
���_�n�̗͊w�֘A�y�[�W
- ���̂̉^��
- ���̂Ƃ́A�C�ӂ̂Q�_�Ԃ̋������^�����Ă���ԕω����Ȃ����̂������܂��B����ɂ��̏ꍇ�A�Q�_�Ԃ̋������ω����Ȃ��̂ŔΘ_�I�Ȓ�`��K�p�ł��܂��B���̂̉^�����l����ꍇ�A���̂̋�ԓI�Ȕz�u���ǂ��Ȃ邩�͂܂���ԓI�ʒu�Ƃ��́g��]�h�����肳����K�v������܂��B