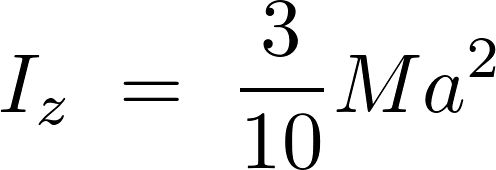円錐の慣性モーメントの計算とその導出過程
初めに(20210619)
当サイトを参考にしてサイト及び動画(youtube)作成・運営している方へのお願い
【社会人として最低限のルール、マナーは守りましょう】
近年、当ドメインコンテンツの明らかな盗用と思われるサイト・動画が一部散見されます。
参考にしたのであれば紹介リンクなどの注釈を入れるといった対応は必ずお願いいたします。
円錐の頂点と底面の中心を通るZ軸周りの慣性モーメント
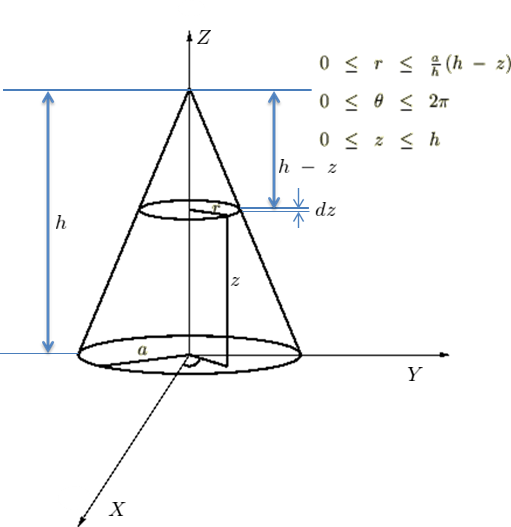
このセクションでは上図のような円錐に関して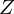 軸周りの慣性モーメントを求めます。
軸周りの慣性モーメントを求めます。
その前にその慣性モーメントを求めるために、まず図中の任意高さ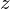 における厚さ
における厚さ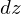 の部分に関しての円錐中にある円盤とみなした部分の慣性モーメントを最初に考えます(円盤の慣性モーメント①と同じ要領ですがここでは距離変数
の部分に関しての円錐中にある円盤とみなした部分の慣性モーメントを最初に考えます(円盤の慣性モーメント①と同じ要領ですがここでは距離変数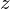 を含む質量を
を含む質量を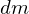 としています)。
としています)。
円盤の対称軸に関する慣性モーメントの計算
円盤の中心軸を通りその円盤に対して垂直な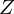 軸の周りを回転する図のような半径が
軸の周りを回転する図のような半径が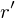 の円盤の慣性モーメントを考えます。
の円盤の慣性モーメントを考えます。

上記画像の円盤の半径は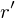 とし、この場合、円錐内の微小厚さ部分の質量としているのでここでは高さ
とし、この場合、円錐内の微小厚さ部分の質量としているのでここでは高さ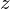 における微小部分質量と考え、この時の微小厚さ円盤の質量を
における微小部分質量と考え、この時の微小厚さ円盤の質量を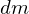 とおくことに注意します。
とおくことに注意します。
座標系は2次元の平面極座標として考えれば、この時の微小部分の面積はヤコビアンによる計算により、
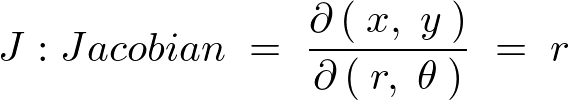
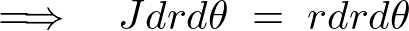
この時の微小円盤質量要素(微小要素の全質量)は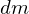 、面積は
、面積は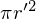 として考えるので微小円盤要素の密度
として考えるので微小円盤要素の密度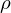 は、
は、
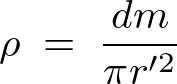
これらによって円錐内の微小円盤要素内のさらに微小部分質量は以下のようになります。
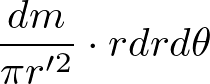
回転軸からの距離は、
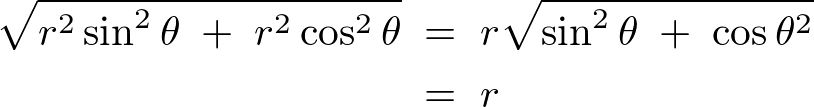
これらにより微小部分の慣性モーメント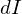 は次のようになります。
は次のようになります。
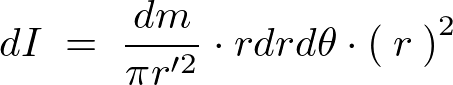
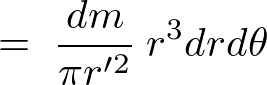
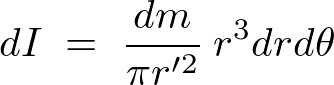
これを積分によって足し上げます。
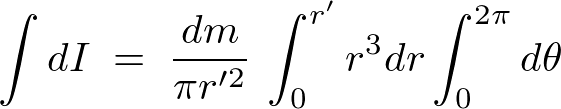
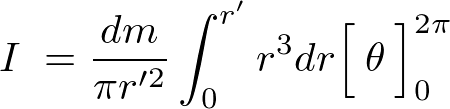
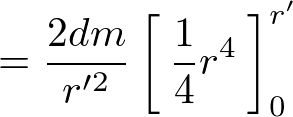
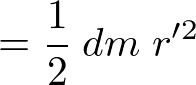
よって円錐内の微小厚さ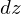 における質量
における質量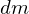 の円盤の
の円盤の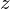 軸周りの慣性モーメントは以下のようになります。
軸周りの慣性モーメントは以下のようになります。
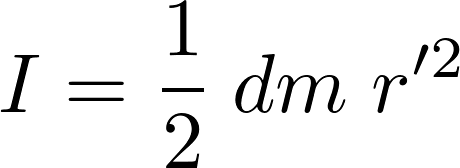
円錐の体積
円柱座標系における円錐の体積積分に関する計算過程
次に円錐の体積を求めます。
円錐の体積を求める場合デカルト座標ではなく次のような円柱座標におけるヤコビアンを使います。
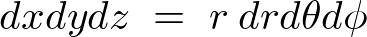
またこの時において(図から)任意高さ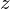 における円錐中の円盤の半径に関する距離変数
における円錐中の円盤の半径に関する距離変数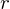 は、相似関係を利用して以下のように求めます。
は、相似関係を利用して以下のように求めます。
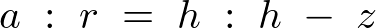
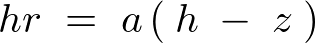
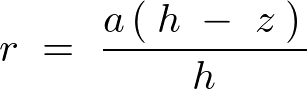
微小体積要素は、
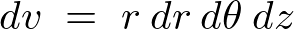
これらにより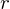 に関しては先ほどの相似関係によって
に関しては先ほどの相似関係によって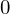 から
から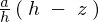 、
、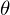 に関しては、
に関しては、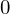 から
から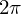 、
、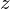 に関しては
に関しては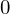 から
から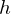 になるので体積積分における重積分式は以下のようになります。
になるので体積積分における重積分式は以下のようになります。
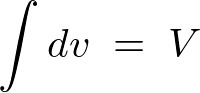
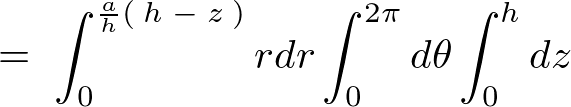
これを計算していきます。
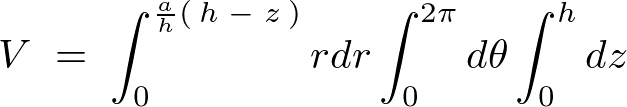
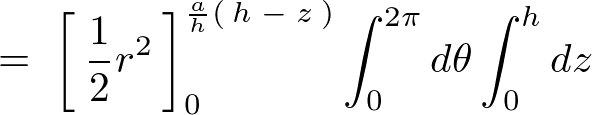
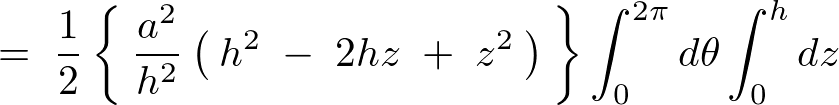
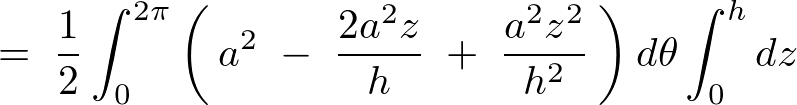
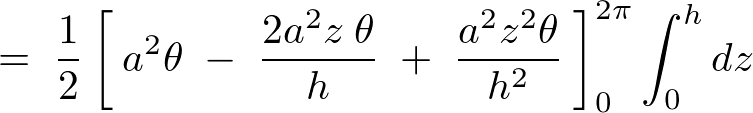
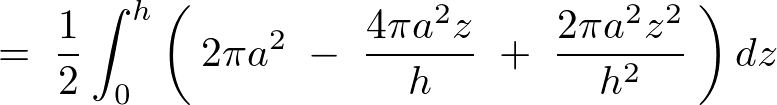
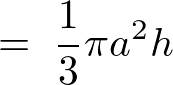
よって円錐に関しての体積計算結果は以下のようになります。
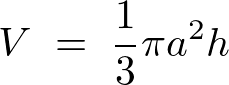
ここから具体的に円錐の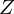 軸周りの慣性モーメントを求めていきます。
軸周りの慣性モーメントを求めていきます。
先ほど求めた円錐の体積と円錐の質量を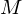 として円錐の体積密度を求めます。
として円錐の体積密度を求めます。
| 円錐の体積 | 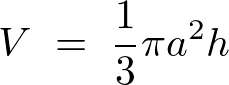 |
|---|---|
| 円錐の質量 | 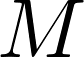 |
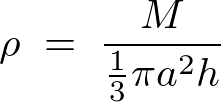
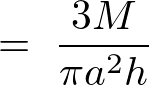
円錐内の任意の高さ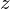 における微小厚さ
における微小厚さ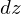 の円盤の
の円盤の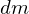 を微小部分の質量、その時の半径を
を微小部分の質量、その時の半径を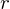 とします。
とします。
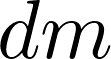 |
任意の高さ |
|---|---|
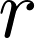 |
任意の高さ |
また更に上記微小部分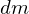 に関しての質量は、
に関しての質量は、
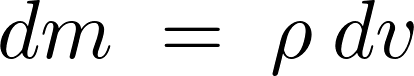
と考えられます。
この任意高さ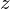 における厚さ
における厚さ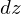 の円盤の微小部分の質量
の円盤の微小部分の質量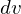 に関してはさらに以下のように面積と厚さの掛け算と考えられます。
に関してはさらに以下のように面積と厚さの掛け算と考えられます。

これにより円錐の任意高さ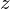 における微小厚さ
における微小厚さ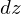 の質量は以下のように表現できることになります。
の質量は以下のように表現できることになります。
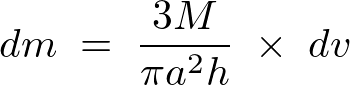
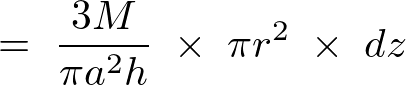
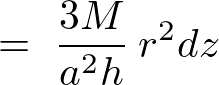
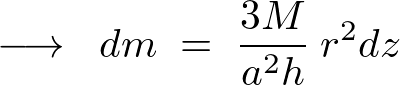
円錐内の任意高さのおける円盤と平行な軸に関する微小部分の慣性モーメント
円錐内にある円盤として考えた部分の慣性モーメントを求めます。
この円盤に関してのz軸周りの慣性モーメントを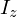 と置きます。
と置きます。
これにより、円盤の微小部分の慣性モーメントは上記の求めた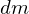 を利用して次のようになります。
を利用して次のようになります。
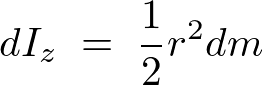
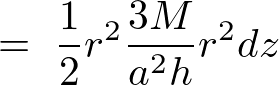
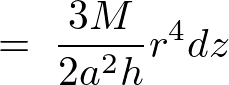
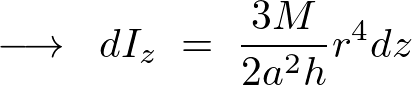
ここで先ほどの相似関係による円錐中の円盤における半径変数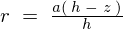 を代入すれば、
を代入すれば、
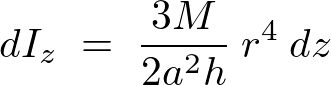
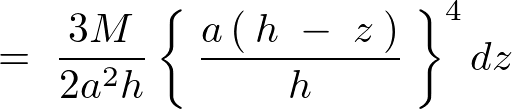
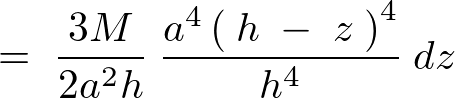
より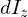 は次のようにおけることになります。
は次のようにおけることになります。
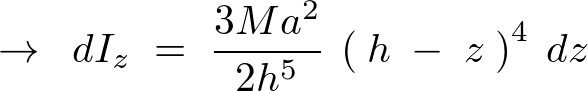
この求まった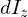 を全体にわたって積分計算していきます。
を全体にわたって積分計算していきます。
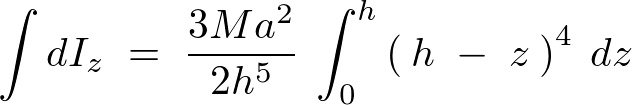
ここで上記積分計算を行うために変数変換をします。
次のように置きます。
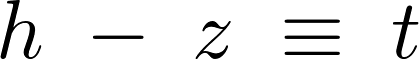
これを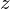 で微分します。
で微分します。
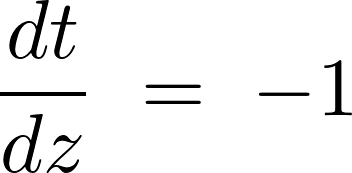
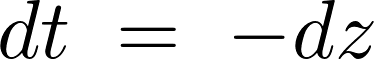
このことにより積分範囲は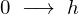 ではなく次のように変更になります。
ではなく次のように変更になります。
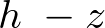 |
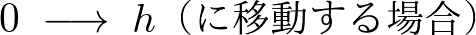 |
|---|---|
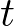 |
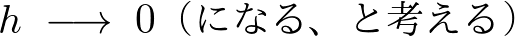 |
よって円錐の慣性モーメントの積分範囲は以下のようになります。
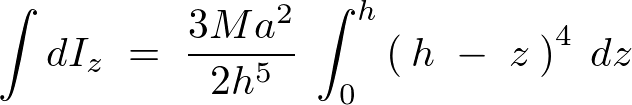
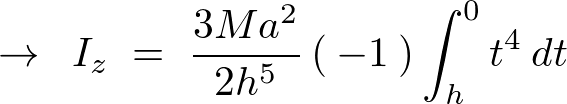
この積分範囲の変更によって積分計算をしていきます。
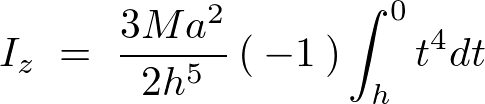
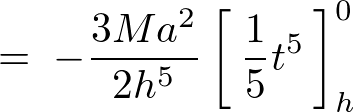
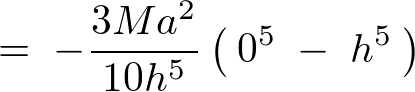
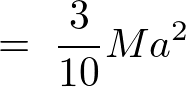
これより円錐の頂点と底面の中心と、重心をを通るz軸周りの慣性モーメントは以下のように求まります。
円錐の慣性モーメント関連ページ
- 長方形板の慣性モーメント
- 長方形板の慣性モーメントの計算。辺の長さ2a、2bの厚さの無い長方形板の重心を通る対称軸に関する慣性モーメント。x、y、z軸のそれぞれにおける対称軸の慣性モーメントをデカルト座標系を使って求めます。
- 直方体の慣性モーメント
- 直方体の慣性モーメントの計算過程。x軸y軸z軸まわりにおけるそれぞれの慣性モーメントを、微小体積要素を求め、さらには微小体積要素部分の慣性モーメントdIをたし上げることにより慣性モーメントを導き出します。使用する座標系はデカルト座標系を用います。
- 棒の慣性モーメント①
- 長さ2aの細長い棒の中点を通り棒に垂直な軸に関する慣性モーメントの計算過程。ディメンジョン1の座標で考え棒の質量はMとします。
- 棒の慣性モーメント②
- 長さ2aの細長い棒の中点を通り棒とαの角度をなす直線に関する慣性モーメント。棒がy-z平面内に含まれるようにし、座標系は極座標系を使用します。さらには軸の方向余弦を求めて角度αをなす直線に関する棒の慣性モーメントを求めていきます。
- 円盤の慣性モーメント①
- 円盤の慣性モーメントの計算過程。半径がR質量がmの円盤に垂直な対称軸に関しての慣性モーメントを求めてみましょう。座標系は2次元の平面極座標を使い、微小面積は極座標のヤコビ計算を行います。
- 円盤の慣性モーメント②
- 円盤の慣性モーメントの計算過程。半径がa質量がMの円盤の中心を通り、円盤の法線をαの角をなす直線に関する慣性モーメントの計算過程。座標系は2次元の平面極座標を使い、方向余弦の直線を考え平面極座標を使って導いていきます。
- 中空円盤の慣性モーメント
- 中空円盤の慣性モーメントの計算過程。内半径がa外半径をbとし、質量がMの中空円盤の中心を通る軸に関する慣性モーメントの計算過程。座標系は2次元の平面極座標を使い、微小部分の質量を求め慣性モーメントを導き出していきます。
- 球の慣性モーメント
- 球体の慣性モーメントの計算過程。質量はM、半径はRの均一な球の中心を通る軸に関する慣性モーメントは極座標を使用して導きます。
- 円輪の慣性モーメント
- 円輪の慣性モーメントの計算過程。質量はM半径はaとし、円輪の中心を通る対称軸に関するx、y、z軸まわりのそれぞれの慣性モーメントを計算していきます。座標系は極座標系を用いて導き出していきます。
- 球殻の慣性モーメント
- 球殻の中心を通る軸に関する慣性モーメントの計算。一様密度で質量がM、外径がb、内半径がaの場合と、球殻の厚さを無視できる場合の2つの慣性モーメントを極座標を用いて導き出していきます。
- 円柱の慣性モーメント
- 円柱の慣性モーメントの計算の具体的な方法。半径がa、高さがl、質量はMとする円柱の重心を通る対称軸に関する慣性モーメントをx、y、zのそれぞれに分けて求めます。使用する座標系は言うまでもなく円柱座標系を用います。
- 中空円筒の慣性モーメント
- 中空円筒の慣性モーメントの求め方。一様密度で質量がM、半径がa、長さをlとし、円筒の外側の厚さが無視できるものとした場合の中空円筒の重心を通る軸に関する慣性モーメントの求め方。
- 半球体の慣性モーメント
- 半球体の慣性モーメントの導出。質量がM、半径がaの半円級の重心を通り底面に平行な軸と、半円級の中心を通る対称軸に関する慣性モーメントを導き出します。
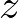 における、厚さ
における、厚さ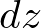 の円盤の質量
の円盤の質量