���s���̒藝�Ɗ������[�����g
���߂Ɂi20210619�j
���T�C�g���Q�l�ɂ��ăT�C�g�y�ѓ���(youtube)�쐬�E�^�c���Ă�����ւ̂��肢
�y�Љ�l�Ƃ��čŒ���̃��[���A�}�i�[�͎��܂��傤�z
�ߔN�A���h���C���R���e���c�̖��炩�ȓ��p�Ǝv����T�C�g�E���悪�ꕔ�U������܂��B
�Q�l�ɂ����̂ł���ΏЉ���N�Ȃǂ̒��߂�����Ƃ������Ή��͕K�����肢�������܂��B
�C�ӂ̓_�O��ʂ�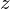 ���̂܂��̊������[�����g�̌v�Z
���̂܂��̊������[�����g�̌v�Z
�d�S��ʂ�P�̎�������Ƃ��A�����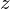 ���Ƃ��āA
���Ƃ��āA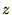 ���̎���̍��̂̊������[�����g��
���̎���̍��̂̊������[�����g��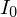 �Ƃ��܂��B
���̎��ɕ��s��
�Ƃ��܂��B
���̎��ɕ��s��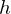 �̋������u�Ă����܂��̊������[�����g���l���Ă݂܂��傤�B
�̋������u�Ă����܂��̊������[�����g���l���Ă݂܂��傤�B

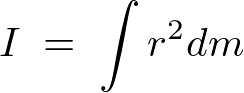
 �_��
�_�� �̎���̃��[�����g�́A
�̎���̃��[�����g�́A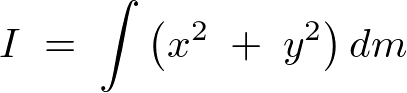
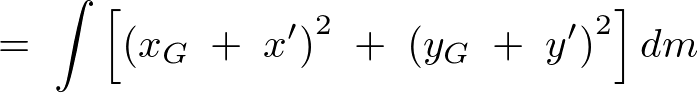
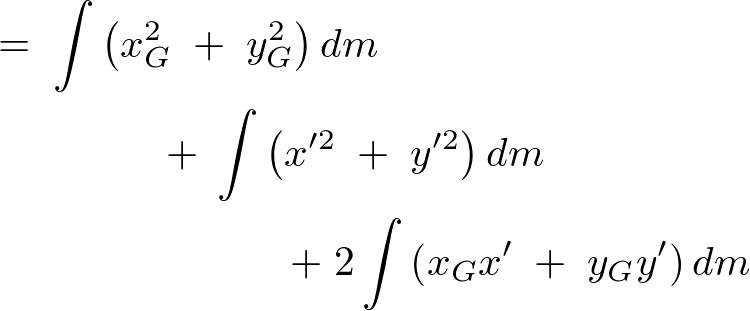
 �����ʒ��S�̍��W�Ƃ��܂��B
�����ʒ��S�̍��W�Ƃ��܂��B�ϕ��̑�Q���͎��ʒ��S��ʂ�A
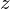 ���ɕ��s�Ȏ��܂��̊������[�����g�ł���A�����
���ɕ��s�Ȏ��܂��̊������[�����g�ł���A�����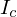 �Ƃ��܂��B
�Ƃ��܂��B
���ʒ��S����]�̒��S0�܂ł̋�����
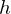 �Ƃ���ƁA
�Ƃ���ƁA
![���ʒ��S����]���܂ł̋���](../img/barycenter_parallel_axis_formula_2022img.png)
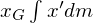 �����
�����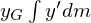 �͎��ʒ��S�̒�`�ɂ����ă[���B
�͎��ʒ��S�̒�`�ɂ����ă[���B
�ȏ�̌��ʂ�芵�����[�����g�Ƃ��āA
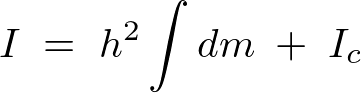
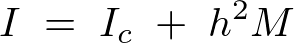
�藝
�C�ӂ̎�����̊������[�����g�́A���ʒ��S��ʂ�A���̎��ɕ��s�Ȏ��̎���̊������[�����g��
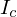 �Ƃ���� �A
�Ƃ���� �A

���s���藝�̊ȒP�ȗ�
���s���̒藝�𗘗p�����������[�����g�v�Z��
�ȒP�ȗ�Ƃ��Ė_�̊������[�����g�����グ�܂��B
�d�S�̈ʒu��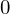 �Ƃ���
�Ƃ���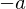 ����
����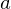 �܂ł̖_�̋����̒�����
�܂ł̖_�̋����̒�����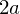 �A����M�̈�l�Ȗ_�̍���
�A����M�̈�l�Ȗ_�̍���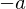 �����ړ������[��ʂ鎲�Ɋւ��銵�����[�����g�����̕��s���̒藝���g���ċ��߂܂��B
�����ړ������[��ʂ鎲�Ɋւ��銵�����[�����g�����̕��s���̒藝���g���ċ��߂܂��B
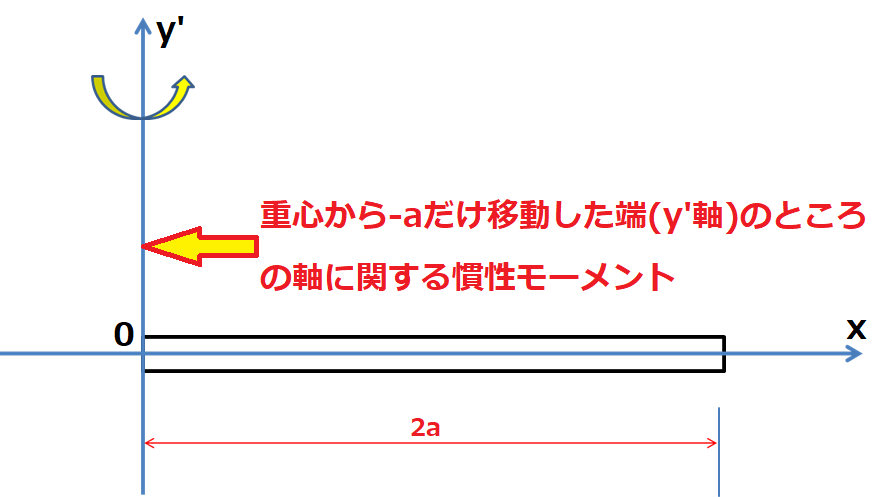
�[�_�Ɋւ��銵�����[�����g�̒��ڂ̓��o
�܂��ŏ��ɕ��s���̒藝���g��Ȃ��`�ł̒[�_�Ɋւ���_�̊������[�����g�����߂Ă݂܂��B
�d�S�̈ʒu��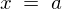 �Ƃ��Ă��܂��B
�Ƃ��Ă��܂��B
���W�n�͉�]����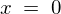 �Ƃ���
�Ƃ���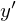 �����Ƃ�A��}����]��
�����Ƃ�A��}����]��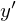 ����蒷��
����蒷��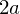 �̈�l�Ȏ���M�̖_�̊������[�����g�Ɋւ���_�̒��S���ł͂Ȃ��[�̕����̊������[�����g�����߂Ă݂܂��B
�̈�l�Ȏ���M�̖_�̊������[�����g�Ɋւ���_�̒��S���ł͂Ȃ��[�̕����̊������[�����g�����߂Ă݂܂��B
���������̒����́A
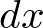
�������v�f�����̖��x�́A
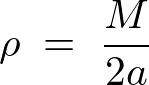
����ɂ����������̑̐ϖ��x�́A
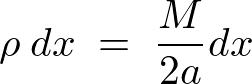
��]������̋����Ɋւ���ϕ��͈͂́A
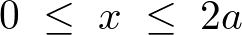
����ɉ�]������C�ӂ̔��������ւ̋����́A
![�_�̉�]������̋���](../img/rod_axis_distance_2022img.png)
�ƂȂ�̂Ŕ������v�f����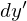 �͈ȉ��̂悤�ɂȂ�܂��B
�͈ȉ��̂悤�ɂȂ�܂��B
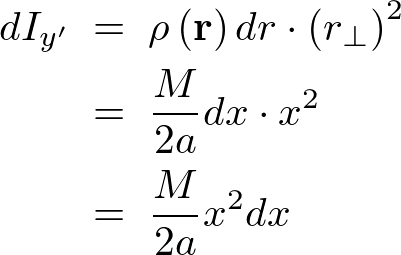
�����ϕ��͈͂� ����
���� �܂ő����グ�܂��B
�܂ő����グ�܂��B
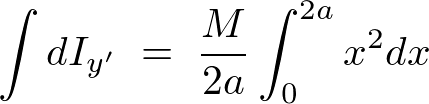
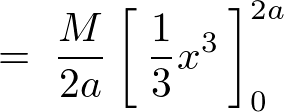
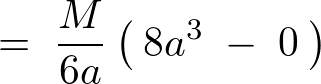
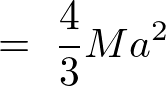
�ƂȂ�̂Œ[�_�ɂ�����_�̊������[�����g�̌��ʂ͂ЂƂ܂��ȉ��̂悤�ɂȂ�܂��B
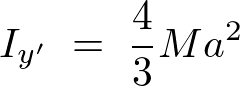
���s���̒藝���g�����������[�����g�̓��o�ߒ�
�V���Ɉȉ��̂悤�ɏd�S��ʂ钆�S���Ɋւ��鎲��y���Ƃ��Ĉȉ��̂悤�ɍ��W�n��u���܂��B
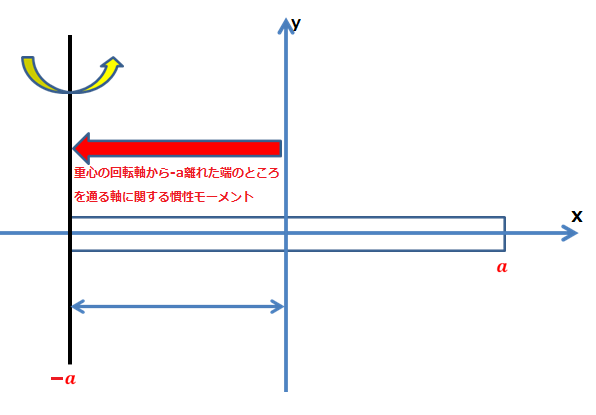
�܂����̖_�̏d�S���Ɋւ��銵�����[�����g�����߂�Ǝ��̂悤�ɂȂ�܂��B
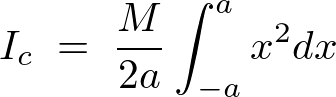
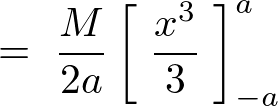
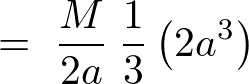
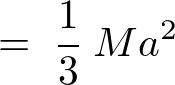
��l�Ȗ_�̏d�S�Ɋւ��銵�����[�����g�̏ڂ������o�ߒ���������
����s���̒藝�ɑ������ƁA
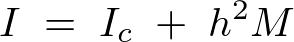
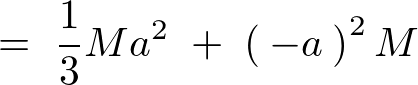
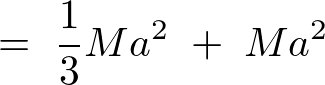
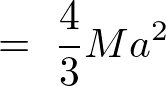
����Ė_�̒��S�����痣�ꂽ�[��ʂ�ʒu�Ɋւ��銵�����[�����g�ȉ��̂悤�ɋ��܂�܂��B
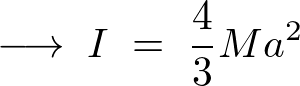
���s���̒藝���g�킸���ڋ��߂��[�_�ɂ����銵�����[�����g�̌��ʂƓ����ɂȂ�܂��B
���̒藝�͕��̂̏d�S�ɑ����]������Ɋւ��Ă̊������[�����g�o�����ۂɁA���̎��ƕ��s�ȔC�ӂ̎�����̊������[�����g�����߂�̂ɖ��ɗ����܂��B
�����܂ł̊w�K�ɂ����Ă͏d�S����̍��̂̉^���̍l�@�𒆐S�ɍs���Ă��܂������A���̒藝���g���ƁA�Ⴆ�������J���Ă���~�Ղɂ����Ă��̏d�S���~�Ղ̒��S��肸��Ă����Ȃǂ̏ꍇ��A�~���̒��_�A��ʁA�d�S����Ɋւ��銵�����[�����g�o����̂ɂ��̈З͂����܂��B
���Ȃ݂ɗ]�k�ɂȂ�܂����ŏ��̋L����yahoo�f���ɂ��̂���ʂ��������[�����g�̎��₪���肻�ꂪ����������2013�N�����������{�T�C�g�ɂăA�b�v���[�h�����̂����������ɂȂ�܂��B






















