くり抜き円盤の慣性モーメント
平行軸定理の応用①
くり抜き円盤の慣性モーメントの導出方法
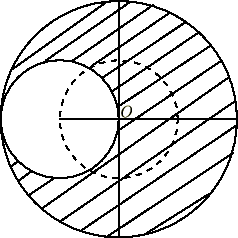
画像の左側の斜線なしの部分は、元の円盤(半径![]() )から半径
)から半径![]() の部分をくりぬいたものと考えてください。
の部分をくりぬいたものと考えてください。
中心を![]() 、半径
、半径![]() の円盤から、その半径を直径とする円をくり抜いた残りの部分の
の円盤から、その半径を直径とする円をくり抜いた残りの部分の![]() を通り、円盤に垂直な軸に関する慣性モーメントを求めます。
を通り、円盤に垂直な軸に関する慣性モーメントを求めます。
考える剛体を![]() 、くり抜く円を
、くり抜く円を![]() 、軸を
、軸を![]() 軸とし、くり抜く前の円盤剛体を
軸とし、くり抜く前の円盤剛体を![]() とします。
とします。
さらに円をくり抜く前の円盤の![]() 軸周りの慣性モーメントを
軸周りの慣性モーメントを![]() 、考える剛体
、考える剛体![]() における軸周りの慣性モーメントを
における軸周りの慣性モーメントを![]() 、さらにくり抜いた円盤剛体
、さらにくり抜いた円盤剛体![]() の
の![]() 軸周りの慣性モーメントを
軸周りの慣性モーメントを![]() とします。
とします。
まず慣性モーメントの定義により次のような式が成り立ちます。
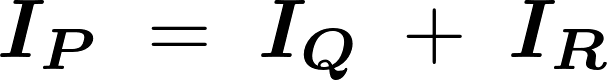
これを変形させると、
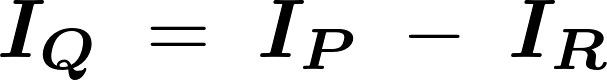
次に![]() を考えます。
を考えます。
円をくり抜く前の円盤の質量を![]() とすると今考えている円盤におけるその面積密度に関しては、
とすると今考えている円盤におけるその面積密度に関しては、
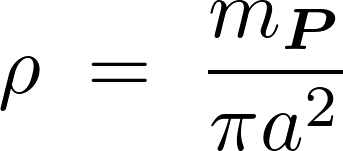
微小面積は平面極座標を使えば、

となるので、微小部分の質量は、
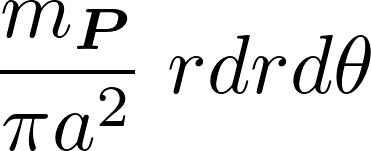
これらにより微小面積要素![]() は以下のようになります。
は以下のようになります。

これらをもとに式を組み立てて計算していきます。
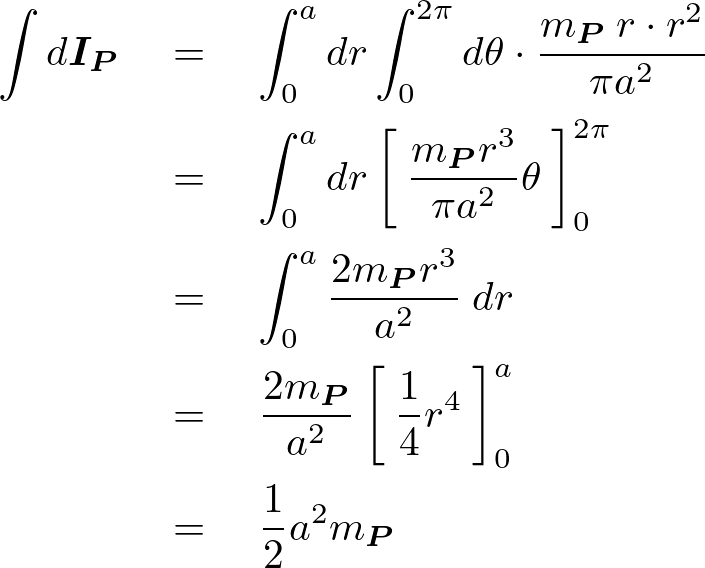
よってくり抜き前の円盤に関する慣性モーメントは以下のようになります。

次に![]() を考えます。
を考えます。![]() の部分の質量は、
の部分の質量は、

であり、この を求めるために
を求めるために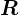 の中心を通り、
の中心を通り、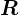 に垂直な軸周りの慣性モーメント
に垂直な軸周りの慣性モーメント を求めます。
を求めます。
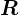 における面積密度は、
における面積密度は、

微小面積は平面極座標系を使用するのでヤコビアンは以下、
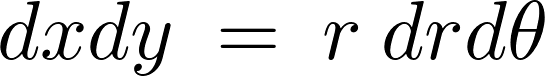
そして軸からの距離は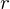 であるので、
であるので、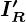 の微小面積要素における慣性モーメント
の微小面積要素における慣性モーメント は以下のようになります。
は以下のようになります。

この積分式を計算していきます。
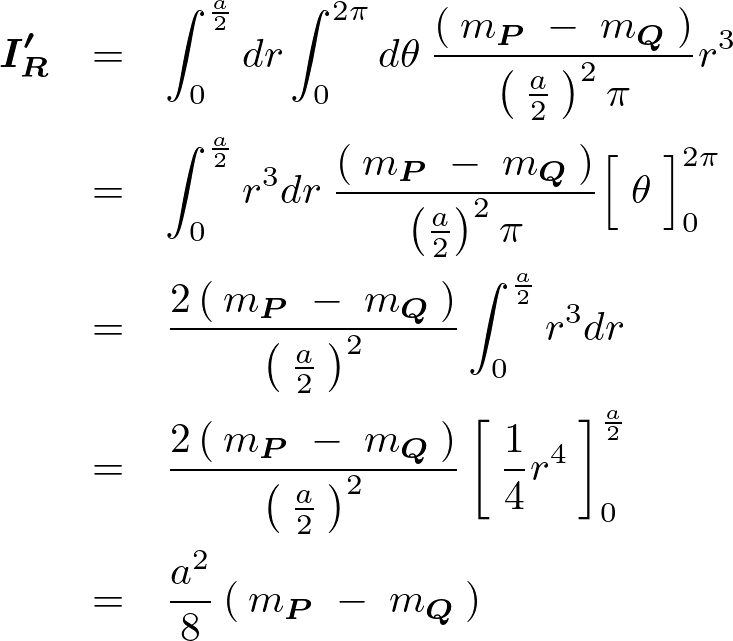
よって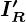 の慣性モーメントは以下のように求まります。
の慣性モーメントは以下のように求まります。

ここで求めたい慣性モーメントは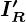 と軸が並行で、距離が
と軸が並行で、距離が![]() だけ離れています。
だけ離れています。
そこで平行軸の定理を使用します。
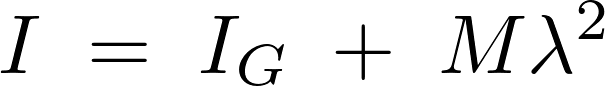
上記の平行軸の定理(シュタイナーの定理)において、左辺の求める![]() を
を![]() 、右辺第1項の
、右辺第1項の![]() が
が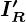 に対応し、そして右辺第2項の質量に当たる
に対応し、そして右辺第2項の質量に当たる![]() が
が![]() 、そして同じく右辺第2項の
、そして同じく右辺第2項の![]() が回転軸からの距離の2乗になるので、結果、次のような式が導かれます。
が回転軸からの距離の2乗になるので、結果、次のような式が導かれます。

それぞれ代入し計算していきます。

よってくり抜いた円盤剛体の慣性モーメン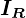 に関しては以下のように求まります。
に関しては以下のように求まります。
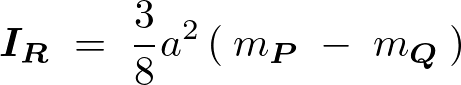
これらの結果により求めようとしているくり抜かれた円盤の慣性モーメント は、
は、
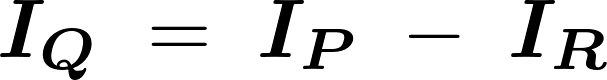
だったのでそれぞれに代入していって計算していきます。
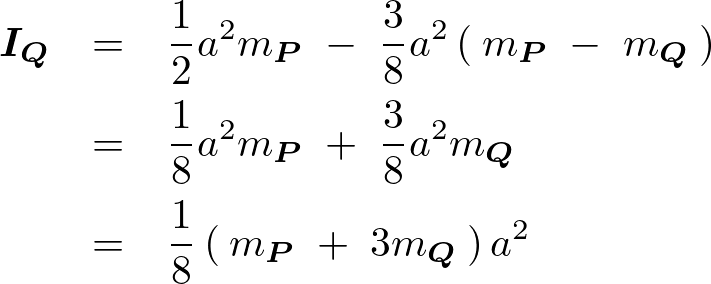
これらの結果により求めようとしているくり抜かれた円盤の慣性モーメント は、
は、

-
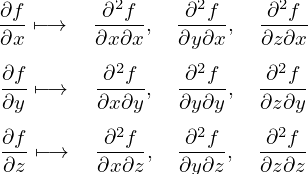
偏微分
カテゴリー
-
導関数
カテゴリー
-

微分積分学
カテゴリー
-
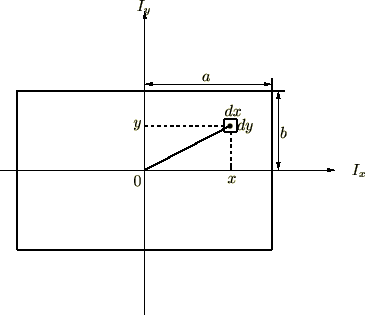
長方形板の慣性モーメント
カテゴリー