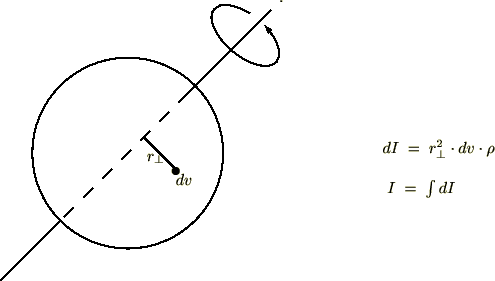質点系と剛体の力学
質点系と剛体の力学
質点系とは多数の質点の集まりを意味し、剛体とは有限の大きさがあり力を加えても変形しない理想的な連続体を示します。
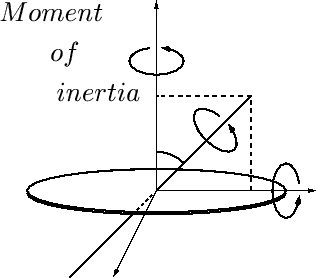
このチャプターでは慣性モーメントを導くための質点系と剛体の力学について考察します。
質点系の力学
複数の質点からなる物理系の内容になります。複数の質点を考えたときそれにかかわる作用反作用の力について考えていきます。
剛体の運動
剛体の運動について。剛体とは任意の2点間の距離が運動しているときに変化しないものをいいます。この時非相対論的定義を適用します。
Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.