長方形板の慣性モーメントの導出過程 ━ 辺の長さがそれぞれ2a,2bの厚さを考えない長方形板の重心を通る対称軸に関する慣性モーメントの計算

直方体の慣性モーメントの導出過程 ━ それぞれの辺の長さを2a、2b、2cとした場合の直方体の重心を通る軸に関する慣性モーメントの計算

棒の対称軸に関しての慣性モーメントの導出過程 ━ 長さ2aの棒の中点を通り棒に垂直な軸に関する慣性モーメントの導出計算過程

棒の慣性モーメントその②の導出過程 ━ 長さ2aの細長い棒の中点を通り棒とαの角をなす直線に関する慣性モーメントの導出過程

円盤の対称軸に関する慣性モーメントの計算 ━ 半径、質量がの円盤を考えます。この円盤の中心を通りその円盤に垂直な軸の周りの慣性モーメント

円盤の慣性モーメントその② ━ 円盤の中心を通り、円盤の法線面上の垂直線とαの角をなす直線に関する慣性モーメントを求めます。

中空円盤の慣性モーメントの導出過程 ━ 中空円盤の内半径をa、外半径をbとします。こうしたときの中空円盤の慣性モーメントを求めていきます。
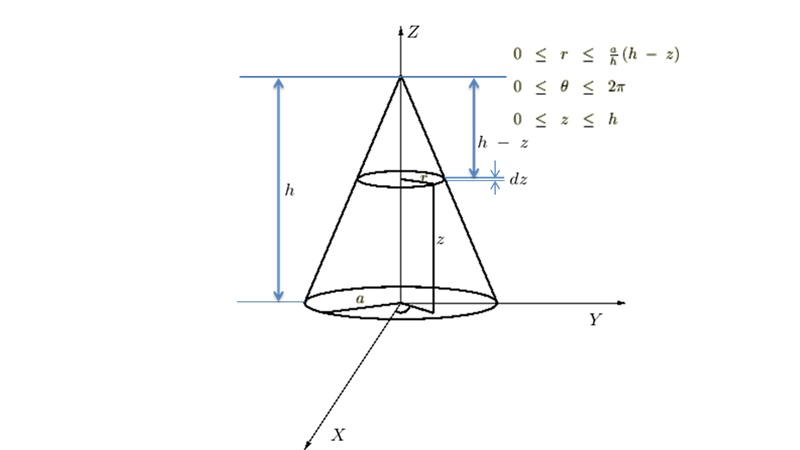
円錐の慣性モーメント ━ ある質点間の距離が変化しない円錐の頂点と、底面の中心を通るZ軸周りの慣性モーメントを求めていきます。

球の慣性モーメントの計算 ━ 球の中心部分となる重心点を通る軸に関する慣性モーメント。考える球体の質量はM、半径はRの均一な球体とします。

円輪の中心を通る対称軸に関する慣性モーメントの計算。極座標系を取り質量はM、半径はa、円周は2πnとしたときのx,y,z軸周りの慣性モーメント

一様密度で質量M、外径b、内半径aの球殻の中心を通る慣性モーメントの厚さがある場合と厚さを無視できる場合の慣性モーメントを考察していきます。

円柱の重心を通る対称軸に関する慣性モーメントの計算 ━ 半径がa、高さがlで質量がMとする円柱のxyz軸におけるそれぞれの慣性モーメント。

中空円筒の重心を通る軸に関する慣性モーメントの計算 ━ 一様密度で質量がM、半径がa、長さをlとし、円筒の外側の厚さは無視できるものとします。
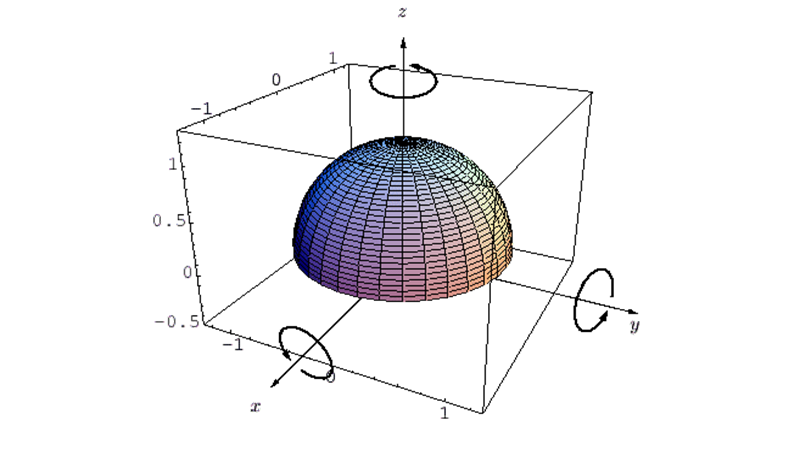
半球体の重心を通る軸に関する慣性モーメントの導出 ━ 質量がM、半径がaの半球体の重心周りに関する慣性モーメントの計算過程。

くり抜かれた円盤の慣性モーメントに関して、平行軸の定理を利用して目的とする円盤の慣性モーメントの導出に関して詳しく解説していきます。
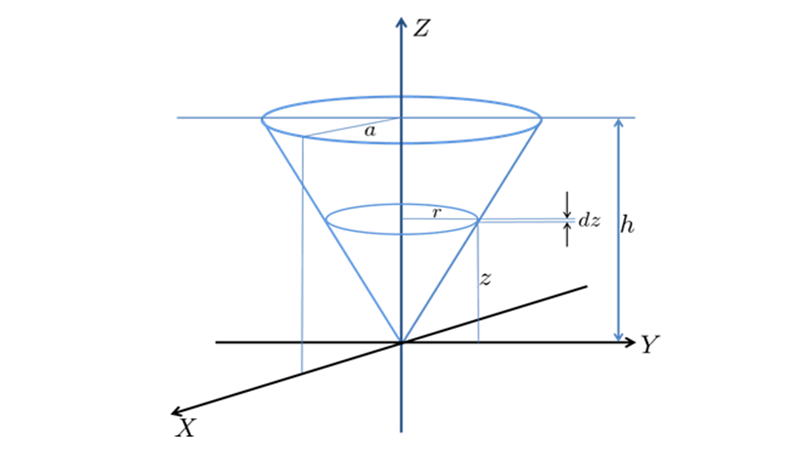
円錐の頂点周り、円錐底面に平行で中心点を通る軸周りの慣性モーメント、さらには円錐の重心回りの慣性モーメントについて考察していきます。

 、質量が
、質量が![]() の円盤を考えます。
の円盤を考えます。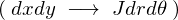 により、
により、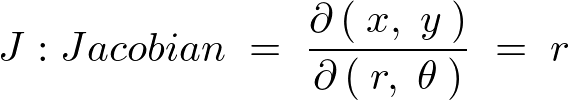

![]() 、面積が
、面積が![]() であるので円盤の密度
であるので円盤の密度![]() は、
は、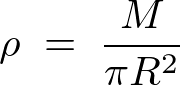
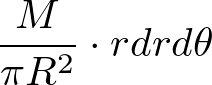
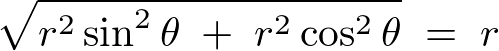
![]() は次のようになります。
は次のようになります。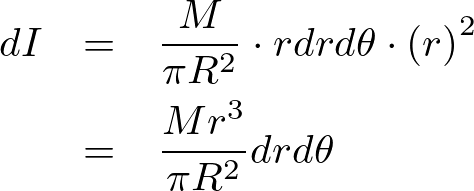
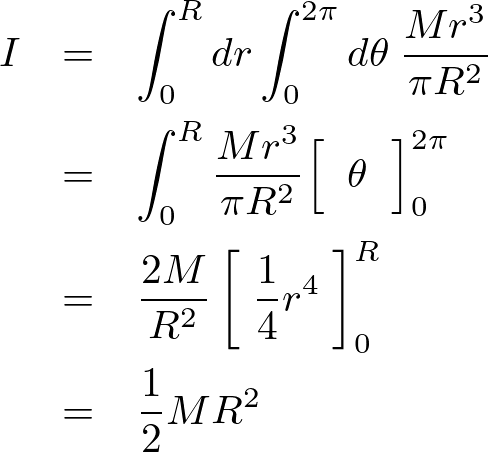
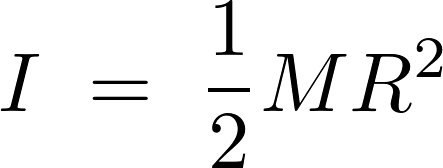
![]() 、半径を
、半径を![]() とします。
とします。![]() 、
、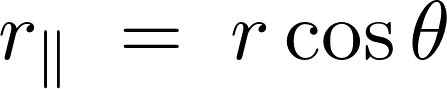
![]() でもかまいません。
でもかまいません。![]() は、
は、