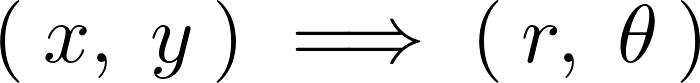変数変換とヤコビアン

ある座標系をほかの座標系へ変えるとき、

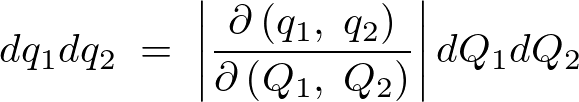
という式が成り立ち、右辺の絶対値で囲まれた部分を具体的にヤコビアン、またはヤコビ行列さらには関数行列式などと言ったりします。
このエントリーでは座標変換に置けるヤコビアンの意味とその役割とは何なのかという事に関して考察していきます。

ヤコビアンとは

ある座標系から別の座標系へ対応させた場合、変数変換を使ってその微小面積要素に対してどの程度のスケール変換量をスカラ倍させれば同値になるのかを求めるものにヤコビアンと呼ばれる数学テクニックがあります。

具体的な例として次のような変数変換における重積分の公式は以下のようになります。

上記式の絶対値で囲まれているがそのヤコビアンに当たります。

一般的に座標系といえばで与えられた場合、通常デカルト座標系といったものを使うと思います。

ここでその座標系に対して新たにといった関数を考えてその変数をとおきそれが変数とは可逆的な関係であるとして次のような式を考えることにします。

上記の関数において平面上の点が平面上のに対応するとした図形を考えた場合、一般的にこれを写像という呼び方をします。

平面上の点を起点にした横の長さ、縦の長さがの長方形の微小面積を考えてその頂点をそれぞれとして、次のような微小面積、

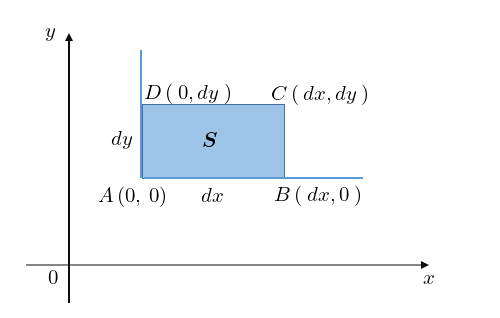
この微小面積における長方形の面積をと置くことにします。

上の図において平面上の点を平面上に落し込んでいった場合、ひしゃげた形の平行四辺形といった形になります。

そこで次のようにといった変化量が近似的に次のような関係性を持っていると考えます。

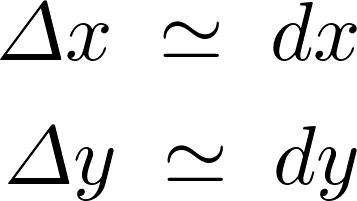
このように考えた場合、それぞれにおけるをで全微分を施すと次のような式が求まることになります。

平面から平面上にそれらを落とし込んでいった場合、ひしゃげた平行四辺形になりますが先ほどのにおけるの微小量の面積が限りなくに近づいていくものと考えます。

そうすると最初はひしゃげた平行四辺形がだんだんと以下のような平行四辺形になっていくと考えられます。

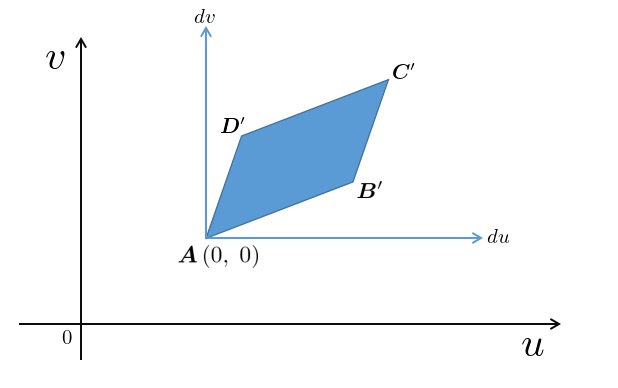
ヤコビ行列式の幾何学的な説明

ヤコビアンの幾何学的な意味を考える場合、まず平面上の点における微小な四角形としたの頂点から始まる面積素分をとし、これに対応するのが平面上の面積素分をとします。

さらにここで平面上の微小面積素分をとし、また平面上におけるその面積をとします。

そうすると、といった面積素分同氏は写像といった対応関係があるので次のような相似関係式が導かれることになります。

上記相似関係の式に関して次のように式変形をしていきます。

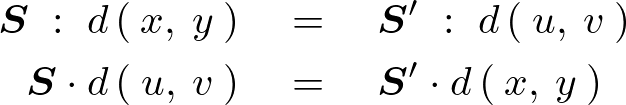
結果として次のような関係式が求まります。

ここで求められた式をよく見てみると左辺の分数部分になっているところはに対してがどの程度の比率になっているかを示していることがわかります。

右辺に関しては変数が多変数になり絶対値を取ってさらに変形すれば以下のような関係式が求まることになります。

上記式において右辺の絶対値を取るのは対応する座標系に対してその値を合わせるためになります。
そして、をを元の微小量変化量に戻せば次のような関係式が導かれることになります。

上記関係式は平面上の微小面積部分の図形が平面上における写像にて写し出された場合における関係性を示すものであり、という面積素分が平面上においてどの程度のスケール変換量になっているかを表しています。

して、右辺の絶対値で囲まれた部分は、単刀直入に言えば平面上における平行四辺形の面積素分になります。

座標系の平行四辺形の面積を求める

平面上の点を平面上のに対応させた場合における新たな座標系の微小面積が等しくなるべくどの程度のスカラー量を作用させればいいかという変換率そのものは平面上における平行四辺形の面積を示していることがわかりました。

次にこの新しい座標系におけるその平行四辺形の面積を求めていきます。

のに関するその座標点は原点のを基準にして次のようになります。

これに対し、新しい座標系における平面上の微小面積における各点の座標は、

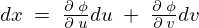
であるので、の座標点は以下のようになります。

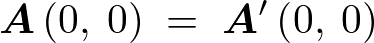
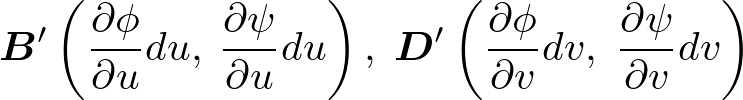
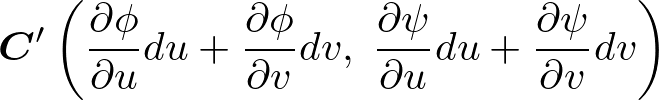
先ほどの平行四辺形の図においてそれぞれの座標点も組み入れれば次のような位置関係になっていることになります。

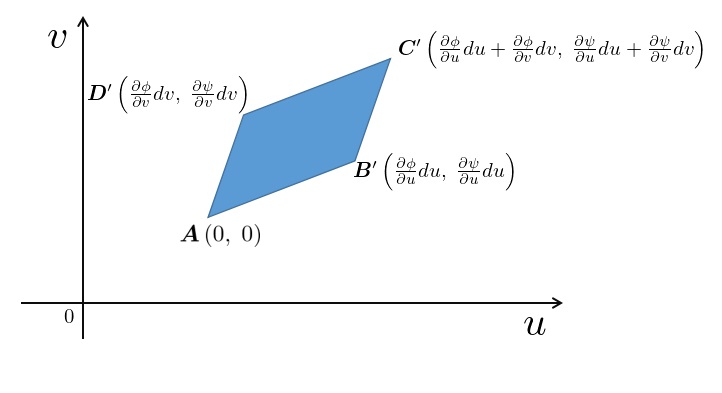
ここからは上図の平行四辺形の面積を線形代数における解析幾何によって求めていきます。

この時において必要になるのが次の３点になります。

この3点を使って図の平面上の平行四辺形の面積を求めていきます。

先ほどの平行四辺形の面積は線形代数における解析幾何によって次のようになります。

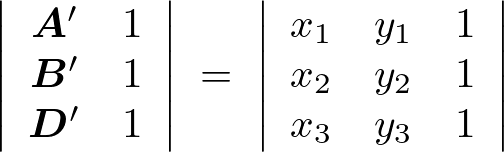
ただしここで（あくまで）便宜上、（多変量ヤコビアンの）理解を促すためのものとして次のように置くことにします。

これに先ほどの値を代入してこの行列式の計算をしていくことにします。

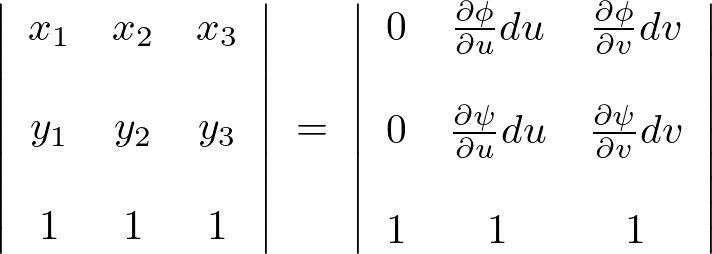
代入すると上記のようになりますが、通常の行列式計算では上のほうから余因子展開していきますがここでも便宜上、かつ計算の簡略化のため行列式の性質より次のように展開して計算していっても特に問題はありません。

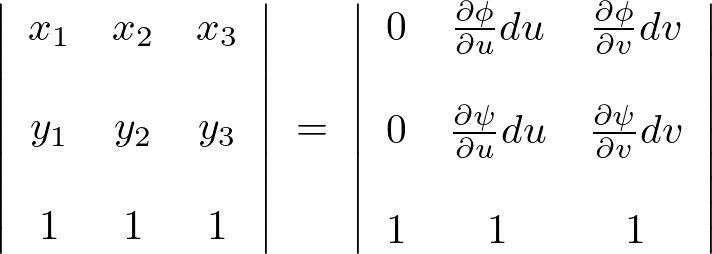
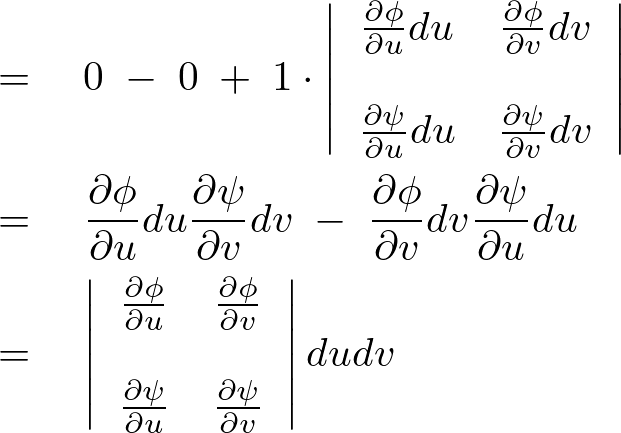
となるので次のような式が導かれることになります。

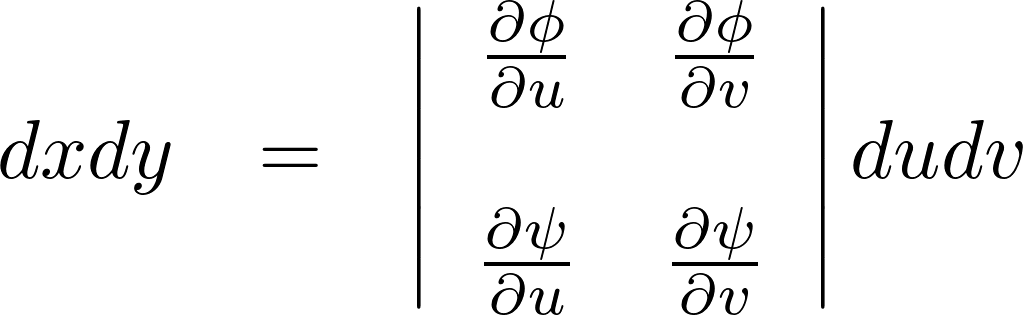
これらの結果によって結局のところ右辺の絶対値で囲まれた部分はスケール変換率に相当する２変数におけるヤコビアン、

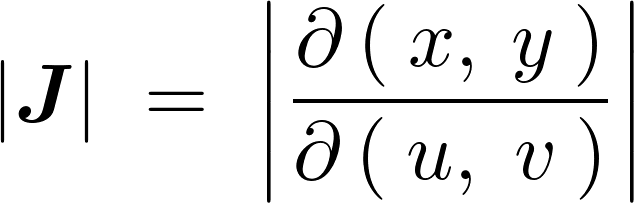
の値に相当することがわかります。

変数変換ヤコビアンによる具体的な座標変換における計算例

具体定期な例としてここでは2変数変換における座標変換で平面極座標を取り上げます。
まず、上記の結果によって導き出された2変数におけるヤコビアンを使った座標変換によるある座標系から考える別の座標系への変換を考える場合、以下のようなヤコビ変数変換をとるものと考えられます。

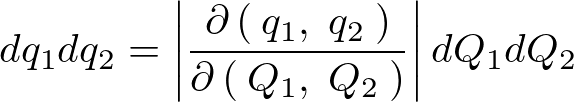
上記座標系において点の位置は、なのでその距離は、

考える座標系は距離とによって決められると考えた場合、その座標系はという座標系に対してどの程度のスケール変換率によって与えられるかということを考えます。