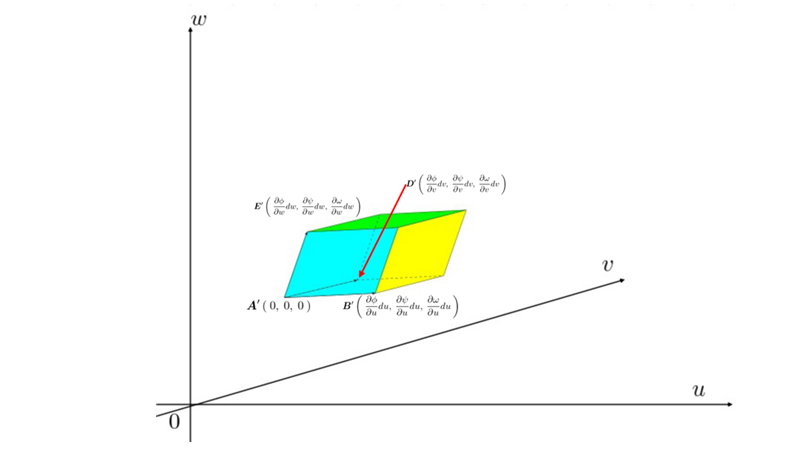
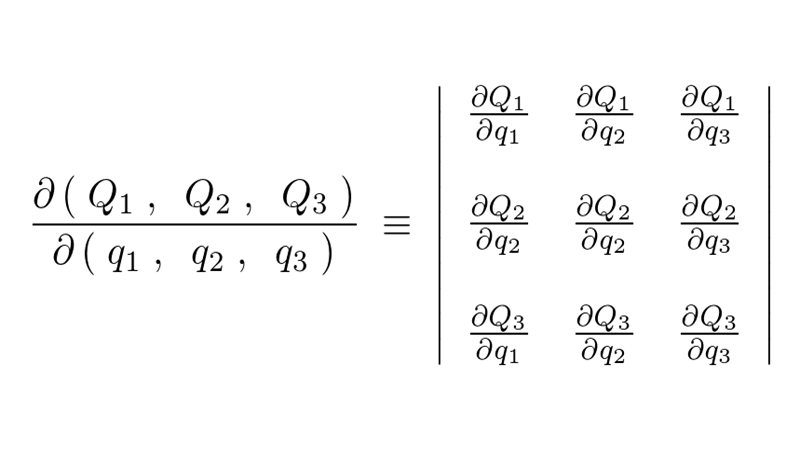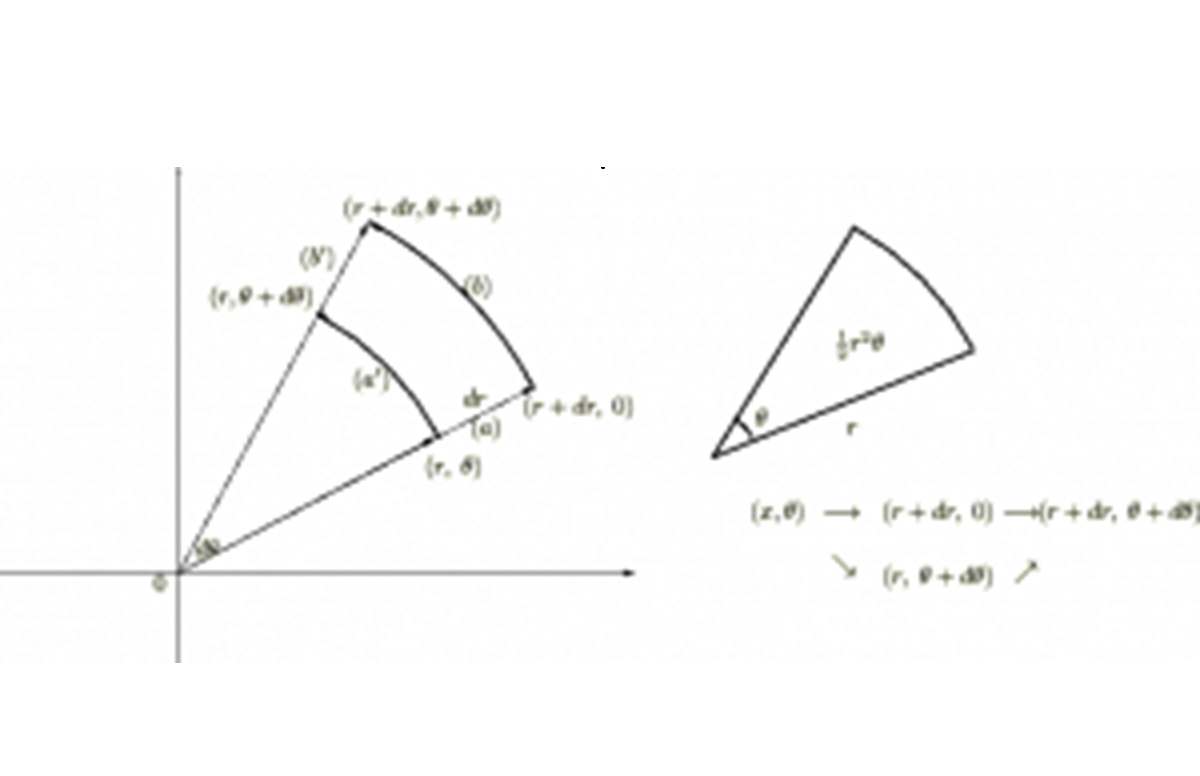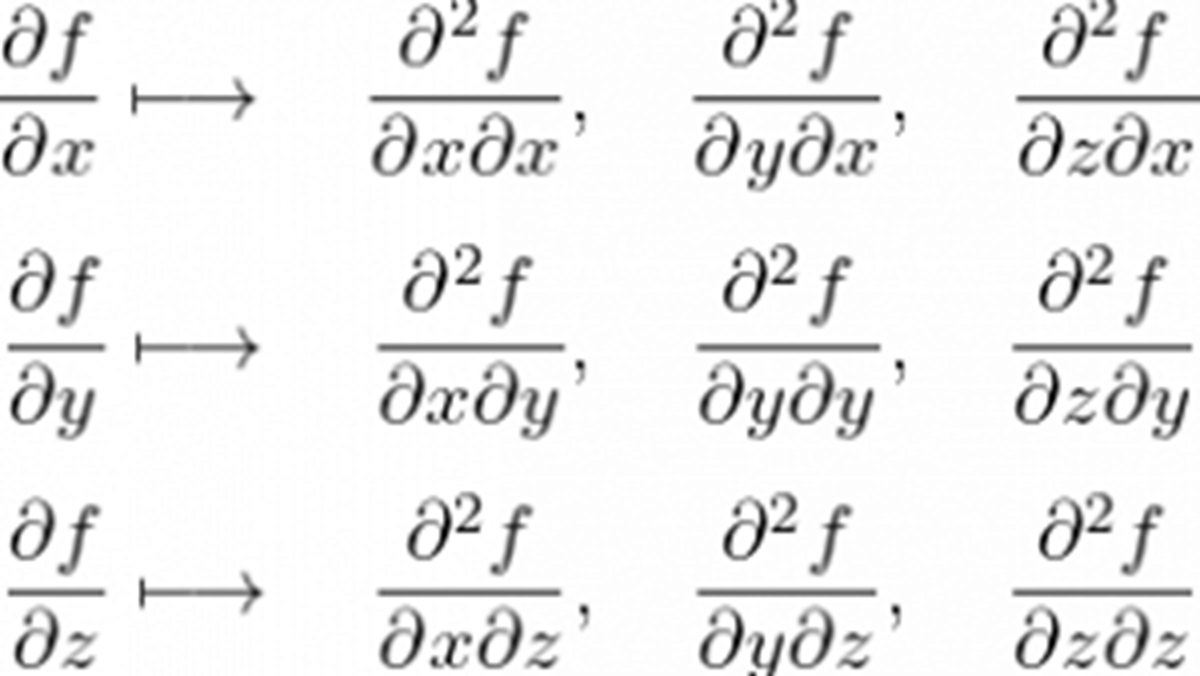先ほどのセクションでは2次元(2変量)における座標変換を考察しましたが、これが3次元または3次元以上の場合のヤコビアンについてはどうなるかを詳しく考察していきます。
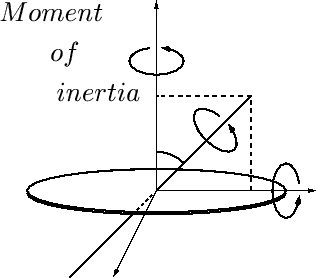
よくわかる慣性モーメント
当サイトを参考にしてサイト及び動画(youtube)作成・運営している者へ。
社会人として最低限のルールとマナーは守れ
近年、当ドメインコンテンツの明らかな盗用と思われるサイト・動画が一部散見されます。 参考にしたのであれば紹介リンクなどの注釈を入れるといった対応は必ずお願いします。

第0章―慣性モーメントの概念
Differential Equations
A differential equation involves an independent variable, its functions, and its derivatives, and has general and particular solutions.

Linear Algebra
Linear algebra is ubiquitous in theoretical physics for those involved in modern science. It is learned in elementary mathematics.
Vector Analysis
Vector analysis is the mathematics of physics by vectors. It is an important theoretical concept used in modern physics.
AKJP Prompt
Want to know more about other matters ? Learn more about knowledge and truth can mitigate burden of mind. Then click here.
回転運動のエネルギー
ある剛体(物体の任意の2点間の距離が変化しないもの)の運動エネルギーは、
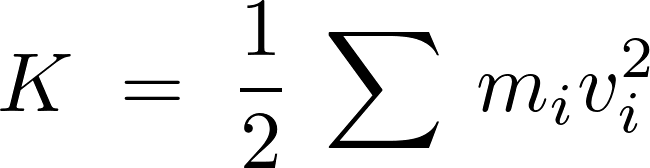
と表され、角速度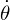 を
を![]() 、つまり
、つまり![]() と置けば、
と置けば、
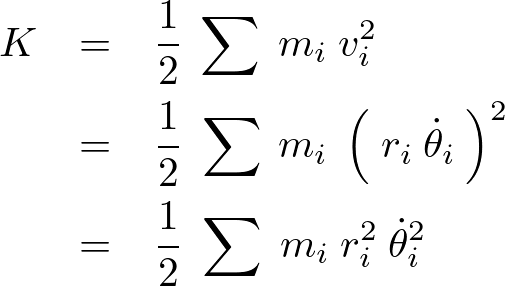
さらに剛体の角運動量(運動量のモーメント)を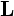 とすれば、
とすれば、
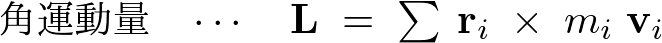
極座標表現により次に示す値、
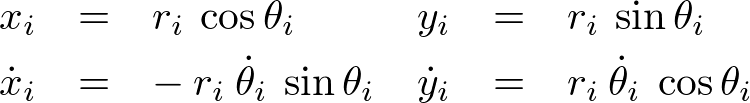
これらを上記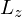 の運動量モーメントに代入すれば、
の運動量モーメントに代入すれば、
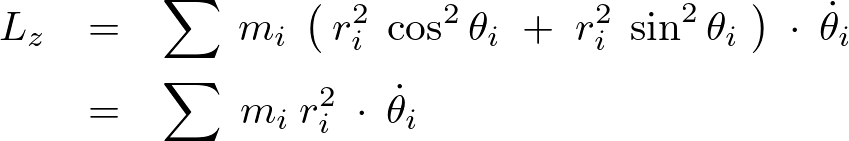
と表現できることになります。
ここで上記の式において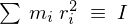 と置けば次のような結果を得ます。
と置けば次のような結果を得ます。

以上に示された記号“![]() ”は、回転軸が決まるとその値が決まります。
”は、回転軸が決まるとその値が決まります。
この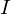 を回転軸まわりの慣性モーメントといいます。
を回転軸まわりの慣性モーメントといいます。
またさらに先ほどの運動エネルギー![]() を考慮すると、
を考慮すると、 であること、及び
であること、及び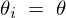 (すべての質点に共通)であるので以下の結果が導かれます。
(すべての質点に共通)であるので以下の結果が導かれます。
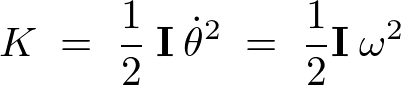
慣性モーメント の求め方
の求め方
次に実際の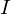 を求める計算として、まず剛体中の微小部分
を求める計算として、まず剛体中の微小部分![]() を考えましょう。
を考えましょう。
 と回転軸までの距離
と回転軸までの距離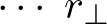
- 剛体の密度

この微小部分の慣性モーメント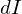 の計算は、
の計算は、

より次のようになります。

この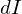 を剛体全体にわたって足しあげれば慣性モーメント
を剛体全体にわたって足しあげれば慣性モーメント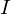 は次のようにもとまります。
は次のようにもとまります。

これらの結果により慣性モーメントとは、簡単に説明すれば物体(剛体)の回転のしづらさ、回りだす変化のしにくさを示す物体の物理的な特性のことだと考えることができるでしょう。
またさらに別の言い方をすれば回転の方程式といえるかもしれません。
慣性モーメント導出の簡単な例
ex.円盤の対象軸周りに関する慣性モーメントの場合
回転軸が円盤の中心を通り円盤と平行な場合の慣性モーメントの計算過程
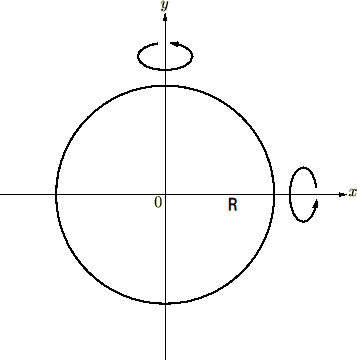
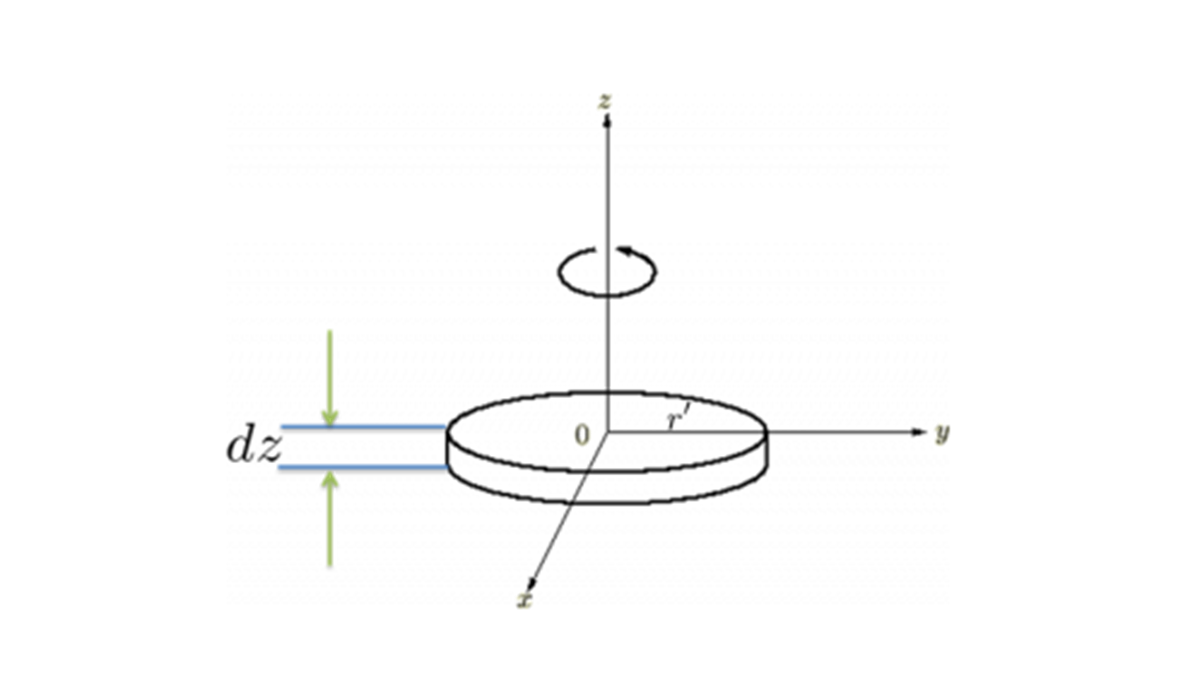
図のような円盤を考えます。
円盤の質量を質量![]() 、半径を
、半径を とします。
とします。
この場合、後述しますがデカルト座標のカーテシャン座標系 ではなく平面極座標を適用しますので微小面積は微小面積要素
ではなく平面極座標を適用しますので微小面積は微小面積要素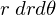 となります。
となります。
さらにこの場合軸からの距離は、

これらにより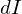 は、
は、
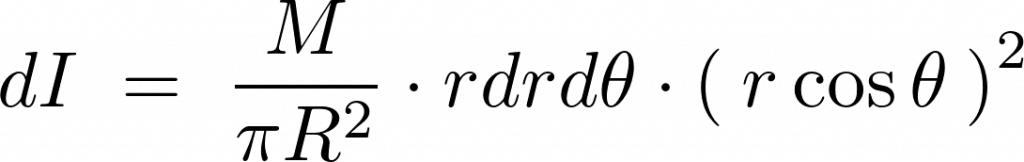
これらを積分によって全体をたし上げます。

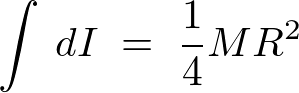
よって円盤面内の重心を通る軸に関する慣性モーメントは、以下のようになります。
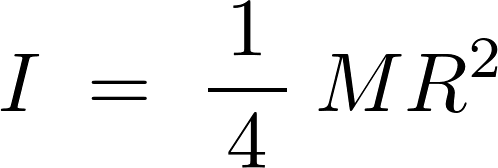
このサイトは主にこの慣性モーメントの求め方と計算法を中心に解説した内容になっています。
その他慣性モーメントを学習・理解する上で欠かせない周辺知識について
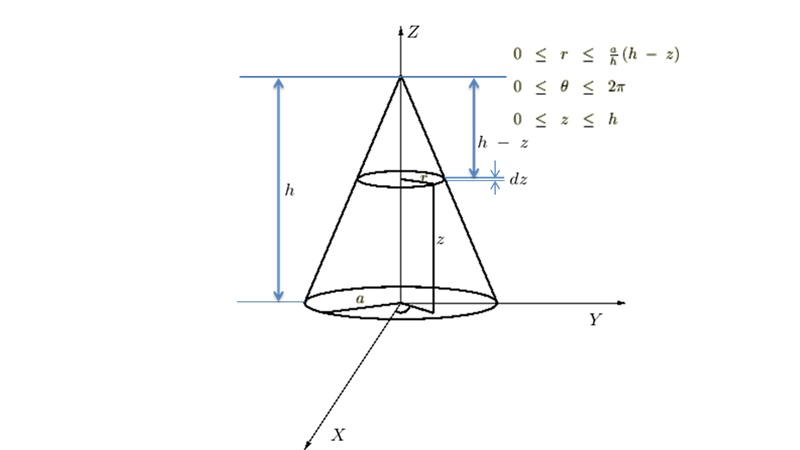
慣性モーメントの計算および導出をする上で欠かせない前提条件としての筆頭として上げられる微分積分に関する知識をはじめとして、円盤および球や、円柱などの慣性モーメントを求める上で重要な知識となる座標変換に関するヤコビアンについてのその考え方と概念の考察、そして質点系と剛体の運動に関する力学についての知識、さらにはくり抜き円盤や、円錐の頂点、底面の中心点を通りその法線面と平行な軸周り、重心周りに関する慣性モーメントを求める上で重要な平行軸の定理に関しても、前半部分(プルダウンメニューの左側)に示しておいてあります。
上述の内容に関しては以下のリンクから目的のチャプターコンテンツをクリックして閲覧していってください。なお上部ヘッダーのプルダウンメニューからのメニュー展開からは、チャプター以下のセクションコンテンツが表示されますので、そこから目的のコンテンツへ入ることもできます。慣性モーメントを理解する上で欠かせない内容になっておりますので自分の力量に合わせながら十分に活用していきましょう。
コンテンツラインアップ
現在アップロードされている物体(剛体)の慣性モーメントの種類は今のところ以下のようになっています。ヘッダーのプルダウンメニューからも目的の慣性モーメントのページに遷移させることもできますが、以下のリンクからも目的の慣性モーメントのコンテンツに移動できます。学習、および参照したい剛体のリンクをクリックして閲覧してください。
このサイトの趣旨
- おもに大学初年度の物理学科の学生を対称としていますが社会人や高校生などの一般の方に対しても微分積分の簡単な説明もあるのであまり無理なく読み進めることが出来るかと思います。
- もともと他のサイトに入れる予定だったものなのですが容量があまりに大きくなってしまい、この調子だと力学なのかそれとも慣性モーメントのサイトなのかわからなくなってしまいそうだったのであえて領域を分けた次第です。それ以外の理由としては他で運営しているサイトのアクセス解析をざっと見渡してみたところどういうわけか半分以上の訪問者の方が慣性モーメントか、あるいはそれに関連するキーワードの検索によって入ってきているという非常に意外なデータがでていること、さらには個人的に不満におもっていたことの理由として現在(2006年の時点)市販されている力学テキストには一般的にありきたりな物(棒、円盤、球などの剛体における対称軸のみの計算)に関する説明のみであることや、またはシスティマティックな計算法を説明した参考書をあまり見たことがなかったものですので今回あえて自分で作ったノートを参考にちょっとだけ教科書風に記述を加えたものをアップロードした次第です。
- 基本的に当サイトでは数学の苦手な方でも理解できることを目的としているので(証明のない数学などはありませんが)わかりづらい表記や説明はなるべく避け、あくまで道具としての数学を習得させることなども目標としています。 内容は慣性モーメントに関する部分だけでなく、最初のほうには慣性モーメントの計算において使用する微分積分に関する簡単な知識、二重積分および三重積分などの重積分法による面積および体積の導出や、平面極座標、極座標、円柱座標におけるヤコビアン(関数行列式)の導出法、さらには力学にちなんだ知識と剛体の重心に関する導出法、またくりぬいた円盤の慣性モーメントや、円錐の頂点、底面の中心点を通る法線面と平行な軸周り、さらには円錐の重心周りの慣性モーメントを求める際に必要になる知識である平行軸の定理などの内容も付け足しておきました。 ページの進め方は上部ヘッダープルダウンより各カテゴリが選択できるようになっており基本的に上から順に読み進めていく感じになります。またヘッダーカテゴリーの微分積分、ヤコビアン…といった部分は慣性モーメントを理解する上での前提条件的な内容でありそこはほぼ蛇足ですので、必要ないという方はヘッダーメニューの“慣性モーメント計算”のほうから閲覧していってください。ちなみにヤコビアン(関数行列式)の導出における行列式の解法は一般的にはサラスを使いますが当サイトにおいては行列式展開法という手法を提示してあります。この計算式の手順に関しては、リンクしてある姉妹サイト“よくわかるベクトル解析”、または“線形代数”のほうを参照なさってください。
無断盗用の禁止事項に関して
近年当ドメインコンテンツの盗用サイト、動画(youtbe)が見受けられます。当サイトにおける文章や画像といったその他も含むコンテンツ関連に関しては無断転載することを一切禁止します。明らかな盗用と思われるものに対しては、法的処置を行います。また引用する場合は必ずバックリンクを貼るなど社会人としての最低限のマナーとルールは守るようにしてください。
お知らせ
- 2024/06/29 ゾーン情報変更不備が原因による不具合が2日ほど継続しておりました。現在は復旧しております。謹んでお詫び申し上げます
- 2024/05/18 SELinuxに対応しました
- 2024/05/17 VPSへマイグレーションしました
- 2023/12/23 円錐の底面、頂点、重心周りの慣性モーメントコンテンツ追加しました
- 2006年より運用開始
-

円盤の慣性モーメント②
続きを読む
-
円盤の慣性モーメント①
続きを読む
-

直方体に関する慣性モーメントの求め方
続きを読む