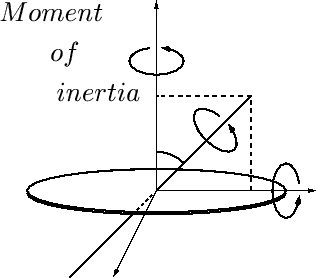
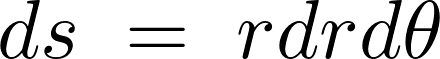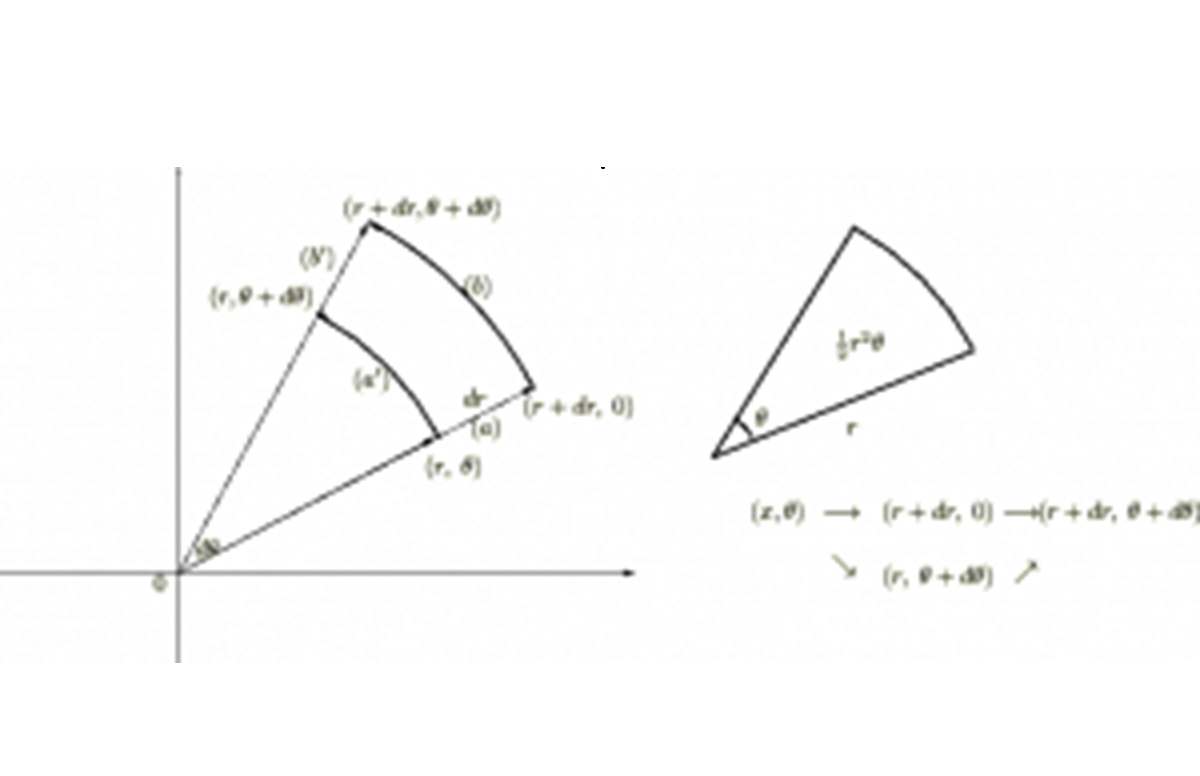重積分学
2変数の積分
形としては次のようになります。
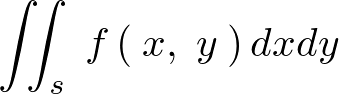
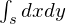 の意味
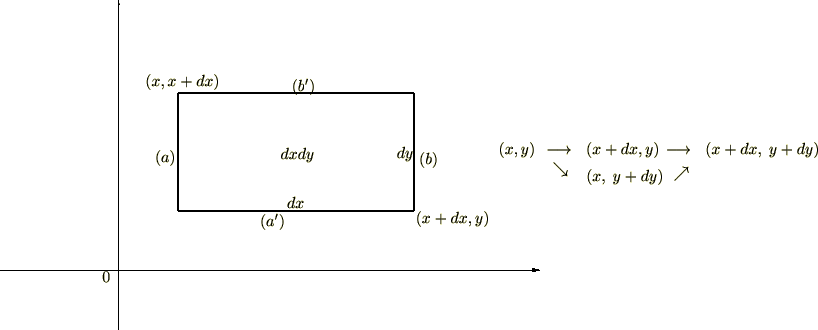
の意味

![]()
![]() は座標系で表現したときの微小面積になります。
は座標系で表現したときの微小面積になります。
ただしこの微小面積は座標系によ
って異なります。
座標系に依存しない形では![]() と書き、先ほどのデカルト表現においては
と書き、先ほどのデカルト表現においては![]() になります。
になります。
ここでこの![]() を図で考えてみましょう。
を図で考えてみましょう。
座標系が![]() のとき、
のとき、
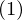 点
点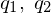 を考える。
を考える。
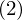 すべての変数を
すべての変数を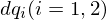 ずらす。
ずらす。
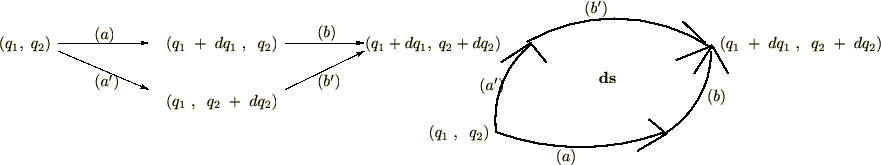
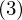 すべての経路によって囲まれた部分の面積が面積要素
すべての経路によって囲まれた部分の面積が面積要素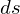 になる
になる
デカルト座標系のでの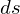
面積要素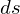 になる。
になる。
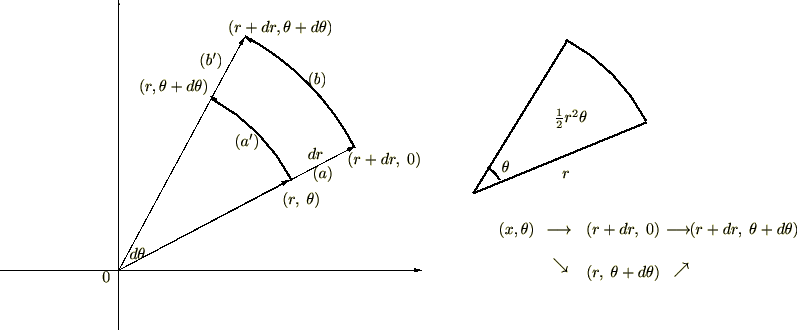
●極座標における微小面積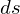 の面積の求め方
の面積の求め方
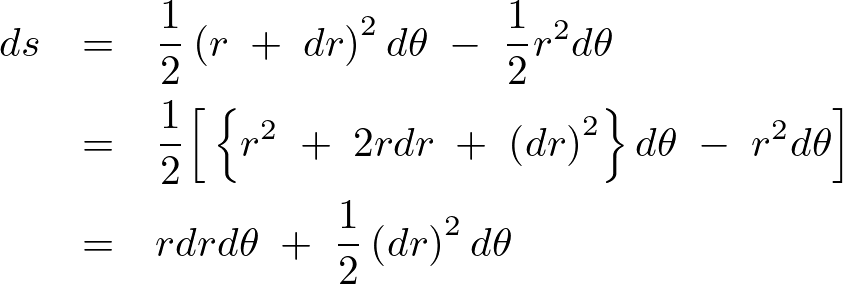
これより以下のようになります。
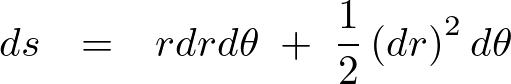
求められた上記の式において、第一項が微少量の2次、第二項が微少量の3次になります。
ひとまず、この場面においては上記の微少量の3次はキャンセルできるとしましょう。
そうすると極座標における微小面積![]() は次のように表現できることになります。
は次のように表現できることになります。