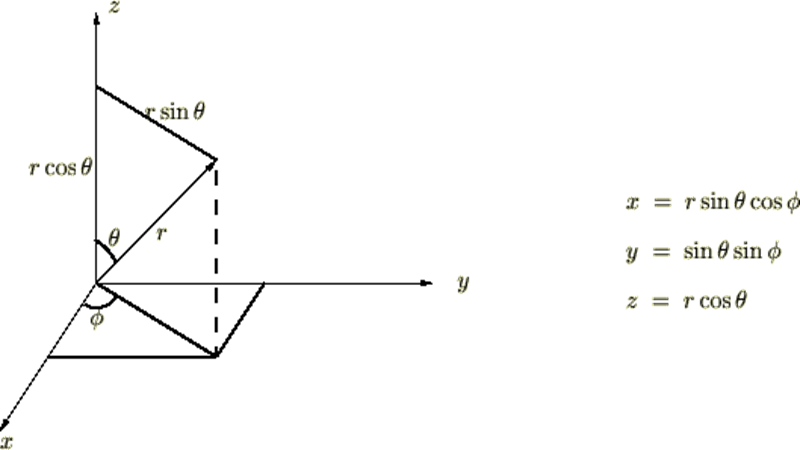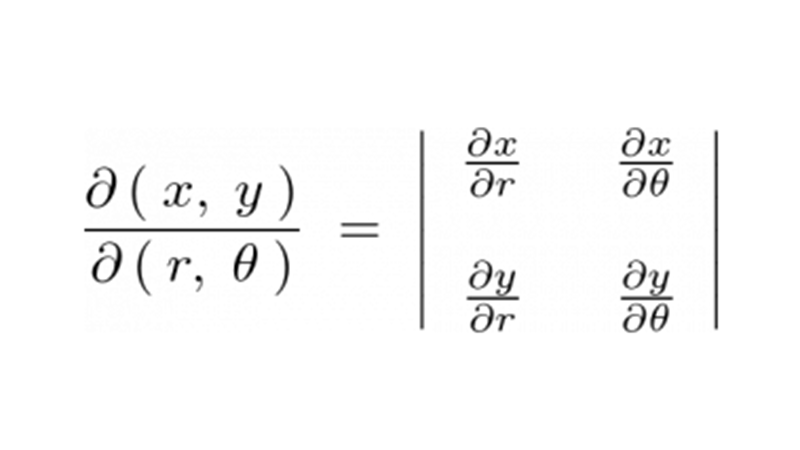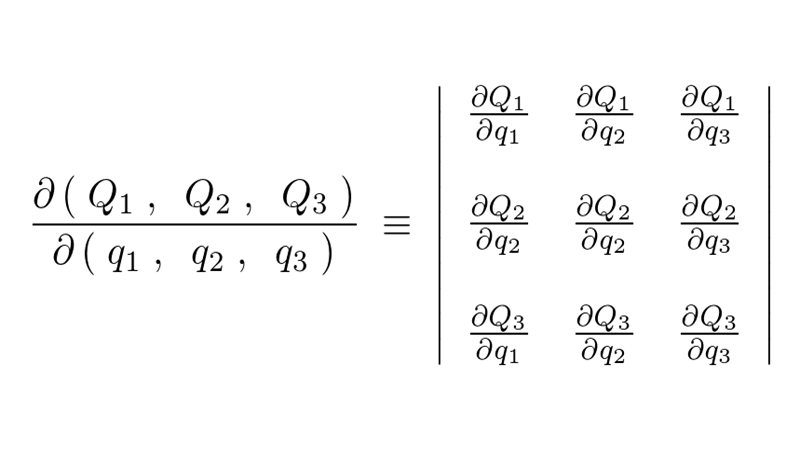ヤコビアン-関数行列式
ヤコビアン-関数行列式
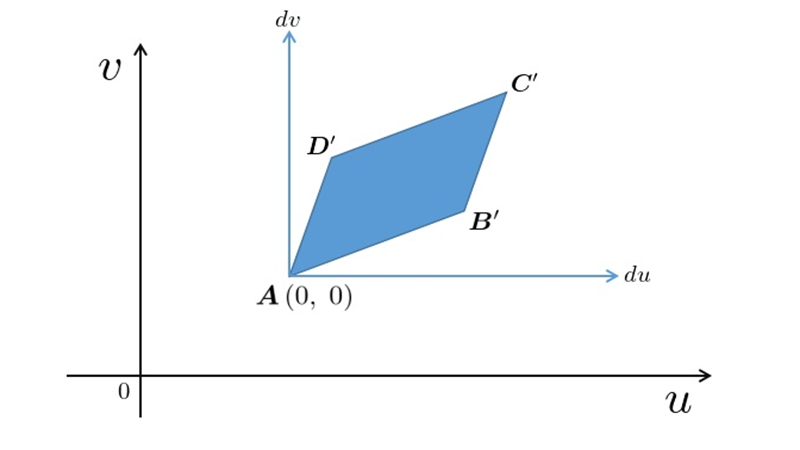
ある座標系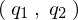 をほかの座標系
をほかの座標系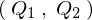 へ変えるとき、
へ変えるとき、
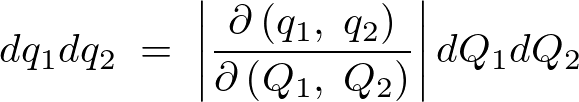
という式が成り立ち、右辺の縦棒で囲まれた部分を具体的にヤコビアン、またはヤコビ行列さらには関数行列式などと言ったりします。なおこの縦棒は絶対値であり、中の分数表示になっている部分は行列式になります。
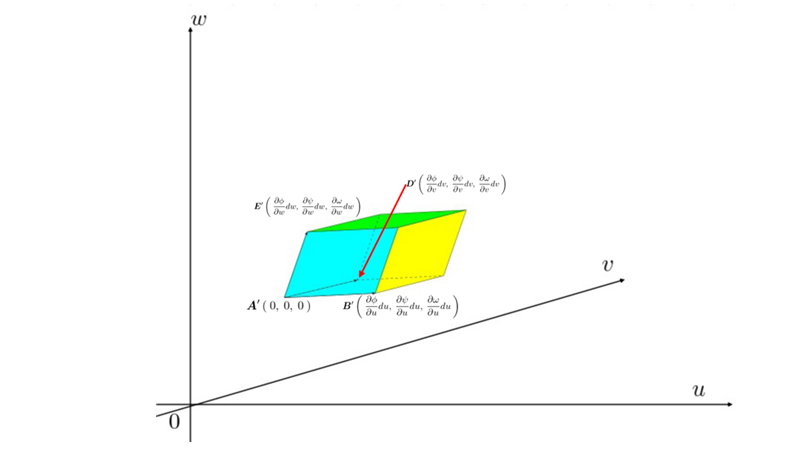
またさらに3次元に拡張していった場合次のようなスケール変換を行って、例えば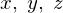 の座標系から別の座標系
の座標系から別の座標系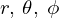 へ変換して微小量体積を変換します。
へ変換して微小量体積を変換します。
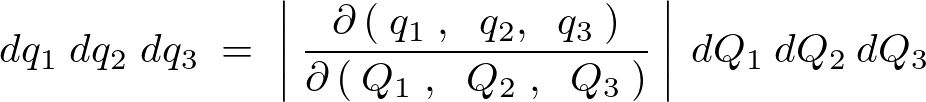
この考え方を拡張していき、3次元以上の場合の多変量解析において重要な考え方になる多変量ヤコビアンについても詳しく解説しています。
このチャプターでは座標変換における変数変換、およびヤコビアンとは何なのか、なぜそうする必要があるのかを詳細に考察していき、極座標、および円柱座標系における慣性モーメントの計算において非常に重要な立ち位置になる座標変換に置けるヤコビアンの意味とその役割とは何なのかについて深堀して考察していきましょう。
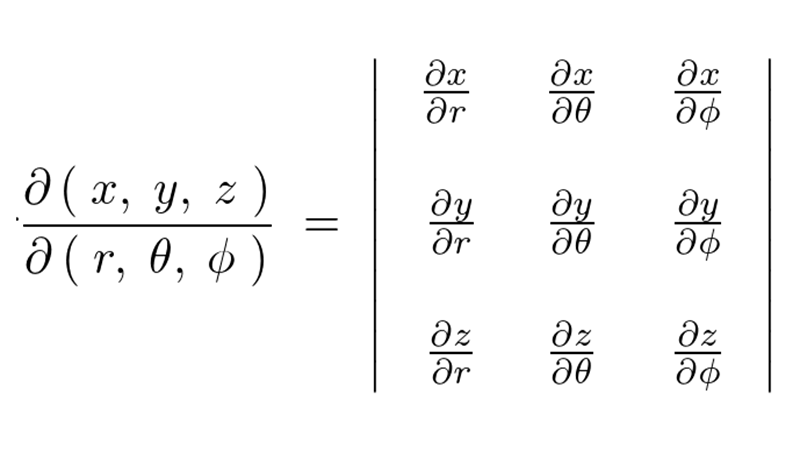
dvの計算法
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

微小体積要素の計算
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
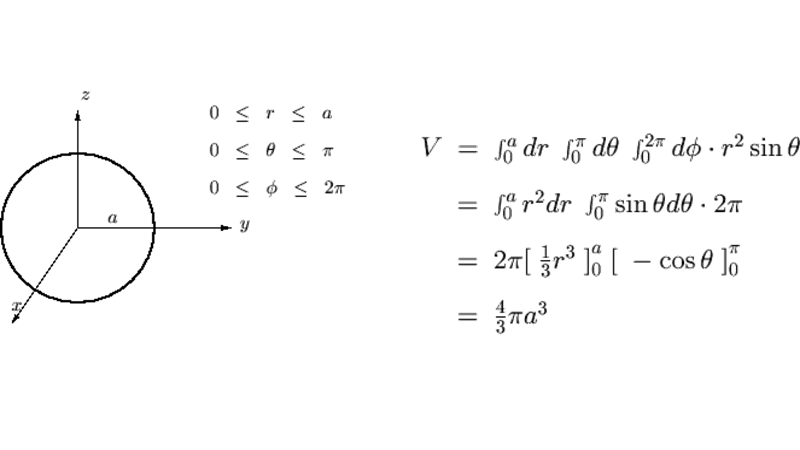
dvの計算方法━答え
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
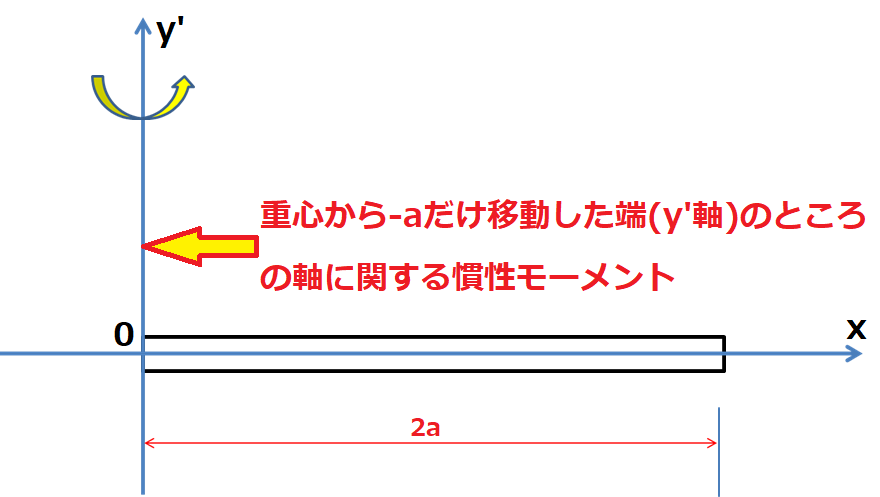
平行軸の定理と棒の慣性モーメント
カテゴリー
-

円錐の慣性モーメント
カテゴリー
-
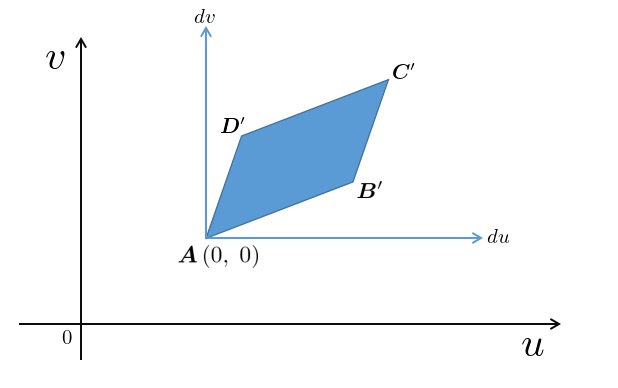
変数変換とヤコビアン
カテゴリー
-

円錐の頂点、底面、重心に関する慣性モーメント
カテゴリー
-

くり抜き円盤の慣性モーメント
カテゴリー
-
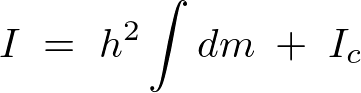
平行軸の定理と慣性モーメント
カテゴリー
-
-
-
-
MOIマイグレーション完全移行完了のお知らせ
カテゴリー : 第2期目マイグレーション完了VPSサーバへの完全移行がとうとう完了しました。2010年代の前半ごろから計画していたものになり、正直行動に移…
-
-
-
平行軸の定理と棒の慣性モーメント
カテゴリー : 平行軸定理を使った棒の慣性モーメント重心の位置を0とする-aからaまでの棒の距離の長さを2a、棒の左へ-aだけ移動した端を通る軸に関する慣性モーメ…
-
-
-
円錐の頂点、底面、重心に関する慣性モーメント
カテゴリー : 円錐の頂点、底面、重心周りの慣性モーメントこのセクションでは平行軸の定理を利用した円錐の頂点周り、円錐底面に平行で中心点を通る軸周りに関する慣性モーメン…