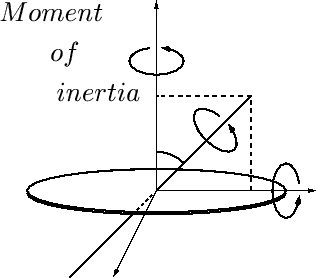
多次元量ヤコビアン
多次元ヤコビアンの考え方とその拡張(加筆編集および査読中)
先ほどのセクションにおいて2次元の場合、ある座標系からほかの座標系に移るとき、次のような式によりスケール変換をすることがわかりました。
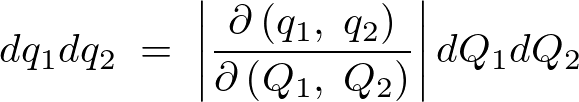
上記式の変換に関しては2つの変数、つまり2次元に関してのものになりますがこれを2次元以上に拡大していった場合どのような定義が導かれるかをこのセクションで考察していきます。
ここではいったん3次元に拡張した場合について考えていきます。
その場合の座標のスケール変換率の式はひとまず次のように表せることになります。
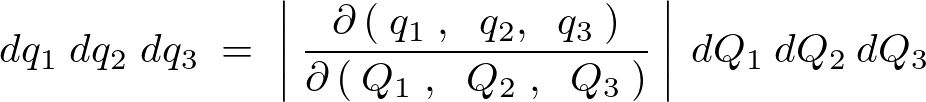
上記の場合、ヤコビアンを利用した重積分の式は次のようになります。
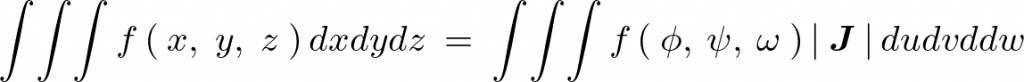
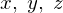 の3次元空間上におけるそれぞれの主要な座標点が今度は3次元になるので
の3次元空間上におけるそれぞれの主要な座標点が今度は3次元になるので になります。このそれぞれの微小位置の各座標点は
になります。このそれぞれの微小位置の各座標点は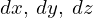 を使えば次のように表すことになります。
を使えば次のように表すことになります。
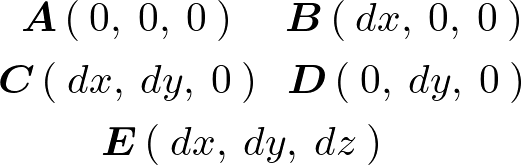
ここにおいても先ほどと同じように 座標系に対して新たに今度は
座標系に対して新たに今度は を追加して
を追加して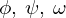 といった関数を考えてその変数を
といった関数を考えてその変数を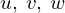 とおきそれが変数
とおきそれが変数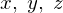 とは可逆的な関係性を持っているとして次のように表します。
とは可逆的な関係性を持っているとして次のように表します。
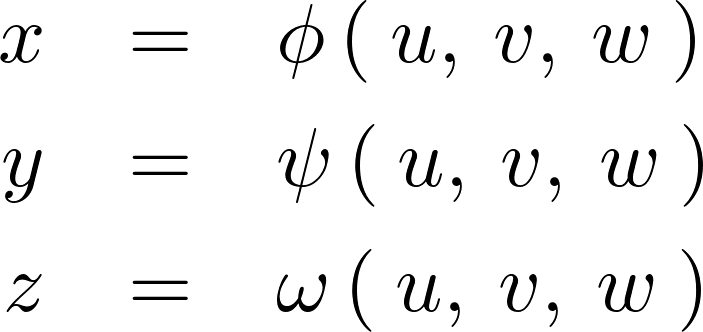
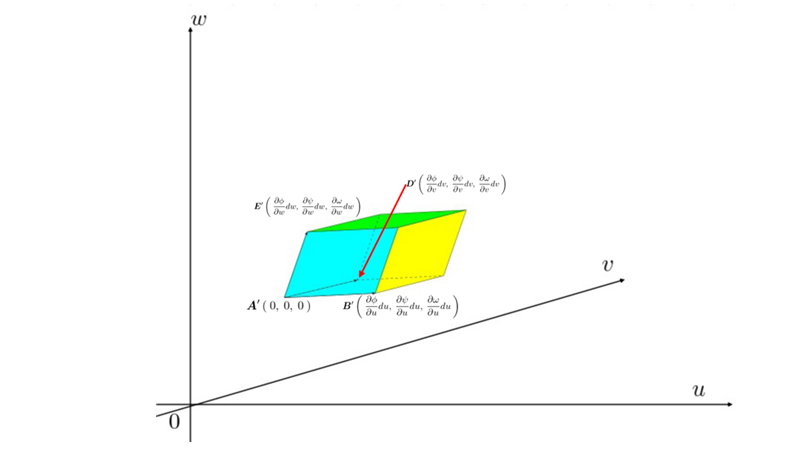
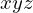 空間上の平行立方体を
空間上の平行立方体を![]() 空間上に落としていった場合、最初はぐにゃっとした決まりのない形に写像されることになります。
空間上に落としていった場合、最初はぐにゃっとした決まりのない形に写像されることになります。
そこで全セクションの2次元の場合でも行いましたがそれと同様に次のような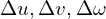 といったといった変化量が近似的に次のような関係性を持っていると考えます。
といったといった変化量が近似的に次のような関係性を持っていると考えます。
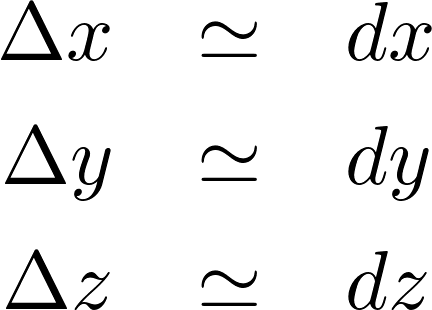
このように考えた場合、それぞれにおける に関して
に関して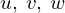 で全微分を施せば次のような関係式が導かれることになります。
で全微分を施せば次のような関係式が導かれることになります。
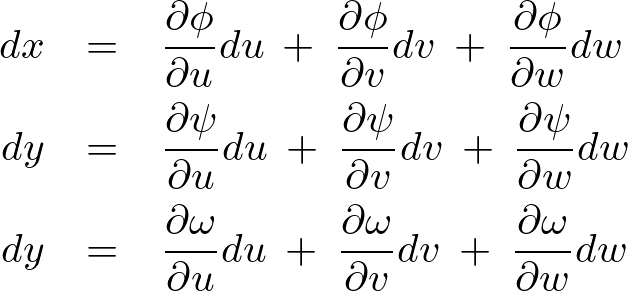
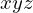 空間上から
空間上から![]() 空間上へ図形を落とし込んでいったとき当初はぐにゃっとした決まりのない形になりますが、先ほどの近似と同様に
空間上へ図形を落とし込んでいったとき当初はぐにゃっとした決まりのない形になりますが、先ほどの近似と同様に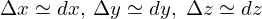 における
における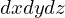 の微小量の面積が限りなく0に近づいていくものと考えます。
の微小量の面積が限りなく0に近づいていくものと考えます。
そうするとぐにゃっとした立方体がだんだんと以下のような以下のような平行六面体になっていくと考えられます。
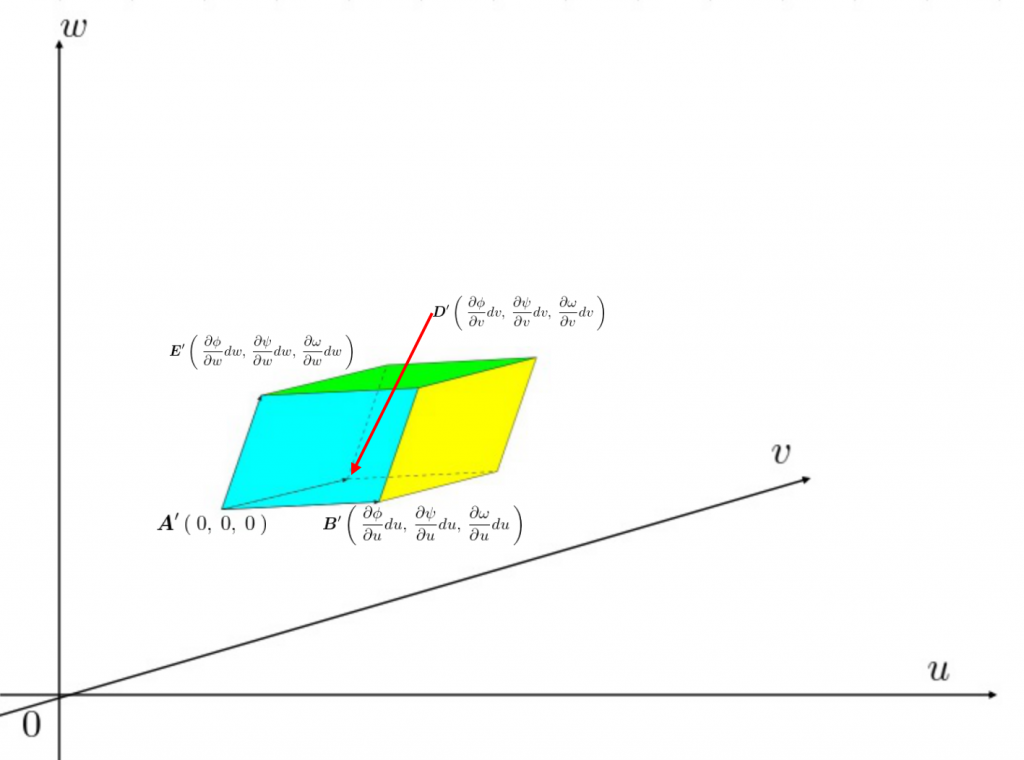
 空間上の平行六面体の面積を求める
空間上の平行六面体の面積を求める
ヤコビ行列に関しての幾何学的な説明は前セクションの内容を参照していただくことにして、ここでは平行六面体の体積を求める方法について考察していきます。
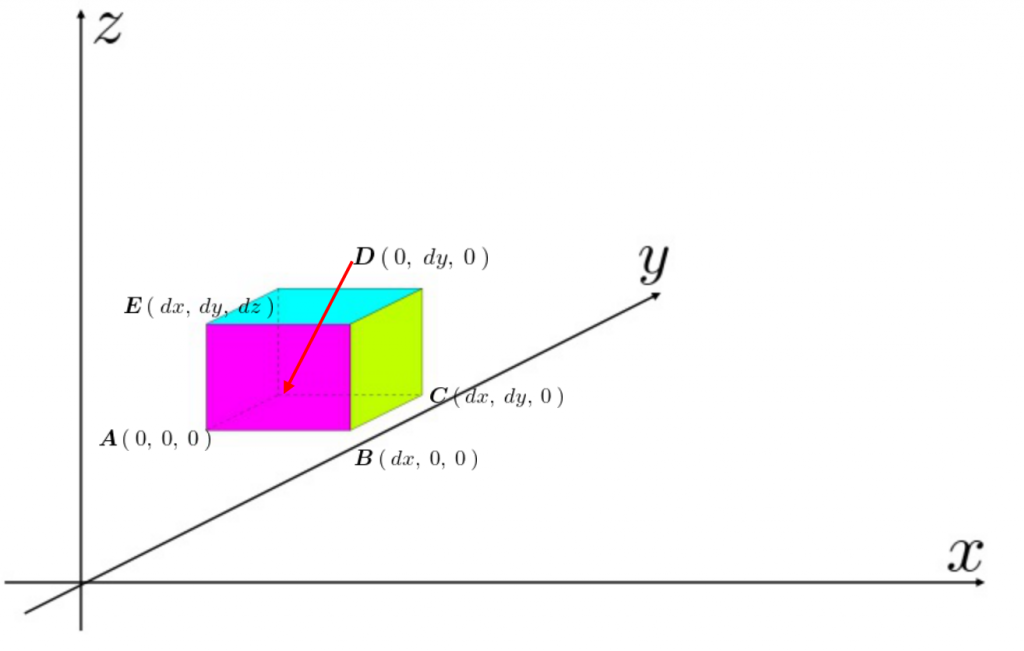
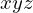 空間上における正六面体を
空間上における正六面体を![]() 上に写像させた場合、
上に写像させた場合、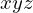 空間のそれが限りなく0に近づいていくものと考えれば上図のような平行六面体になり、この新たな座標系におけるスケール変換率がこれに相当します。
空間のそれが限りなく0に近づいていくものと考えれば上図のような平行六面体になり、この新たな座標系におけるスケール変換率がこれに相当します。
この新しい座標系におけるその平行六面体の体積を求めていきます。
新しい座標系における平行六面体のそれぞれの座標点は以下のようになります。
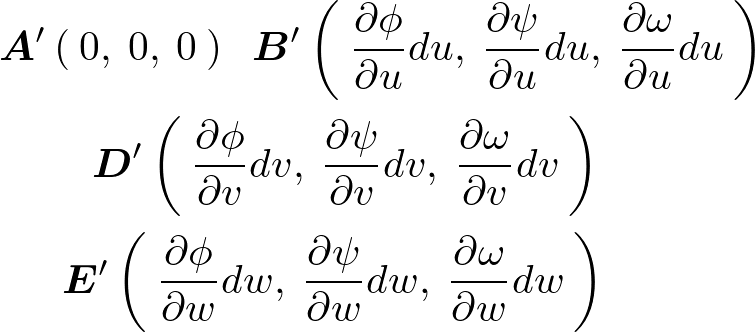
この4点を使って上図の平行六面体の体積を計算していきます。
全セクションと同様に行列式によってあらわすと次のような表現になります。
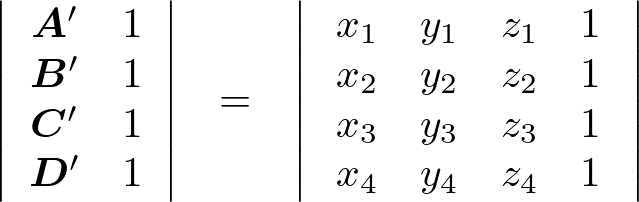
ここでも便宜上次のようにおくことにします。
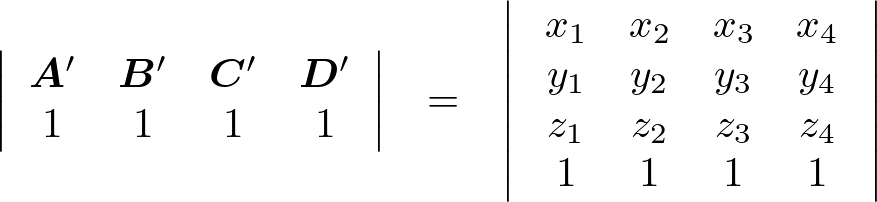
これに値を代入して次のように計算していきます。
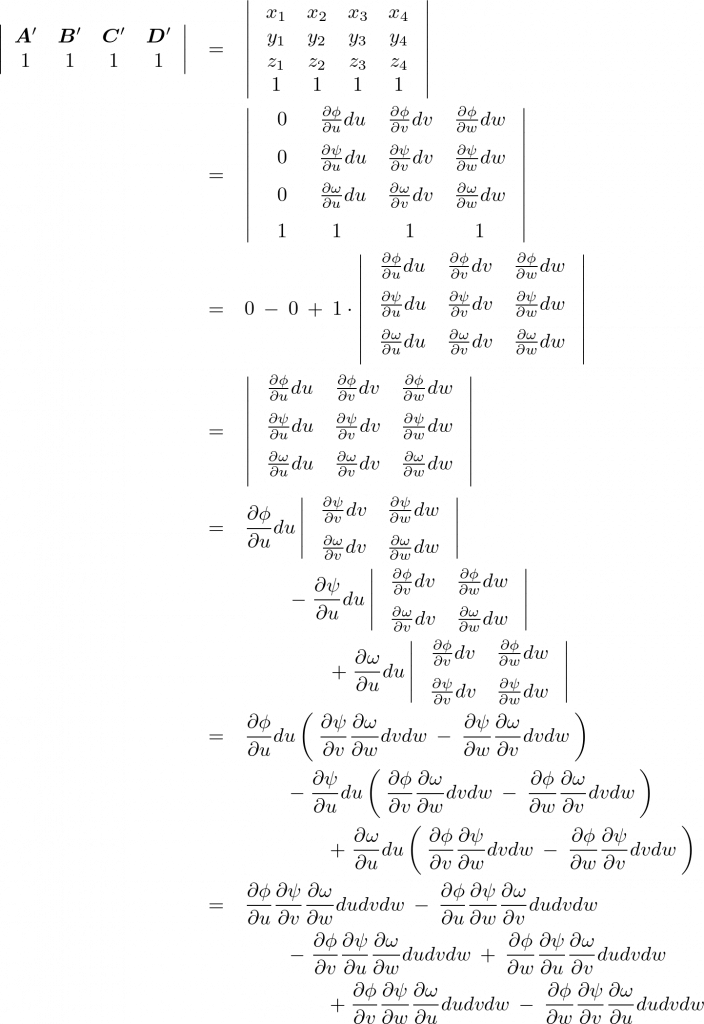
となるのでまとめてみると次のようになります。
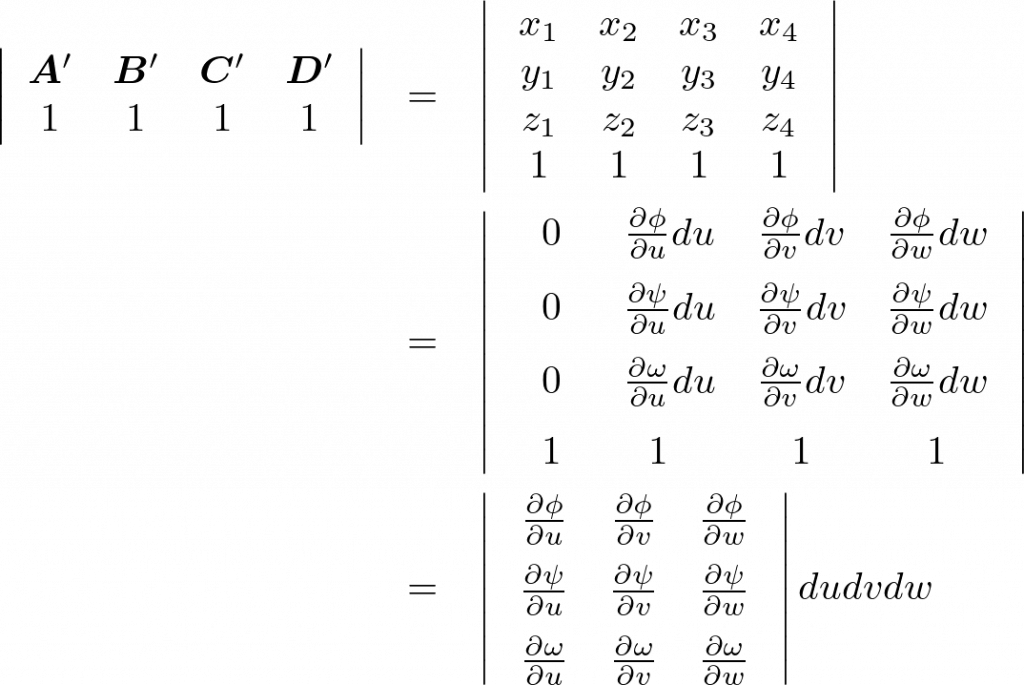
結局のところ2次元から一つ次元を増やした場合の3次元におけるヤコビアンについて、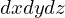 座標系から
座標系から![]() 座標系へのスケール変換率の場合は以下のような式が求まることになります。
座標系へのスケール変換率の場合は以下のような式が求まることになります。
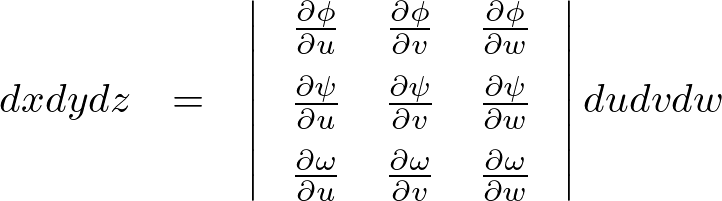
この結果により2次元から一つ次元を増やして3次元にした場合においても、上記のように行と列にそれぞれひとつづつ変数を増やした形のヤコビアンになっていることがわかると思います。さらに次元を増やしていっても同様のことがいえることになり、次のような形におけることになります。
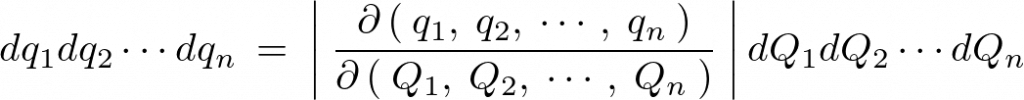
行列の形を“便宜上”として形を変えた理由はこういった事を理解するための梯子としていたからになります。