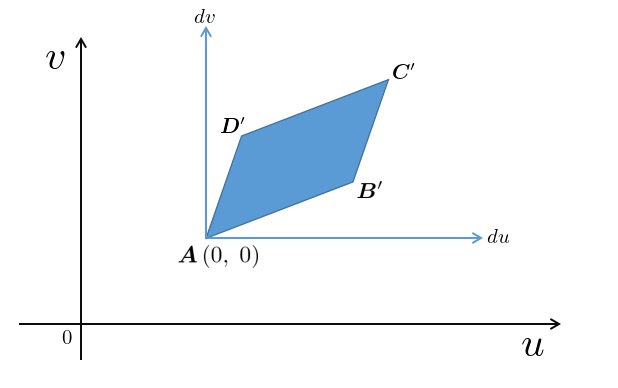
微小体積要素dvの計算
微小体積要素dvの計算問題
先ほど求まったそれぞれの座標系におけるヤコビアンを使って実際の体積積分計算を行っていきましょう。
問題①
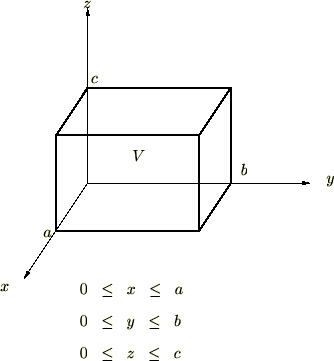
次に示す直方体の体積を三重積分によって求めてみましょう。
問題②
半径![]() の球の体積を極座標で求めてみましょう。
の球の体積を極座標で求めてみましょう。
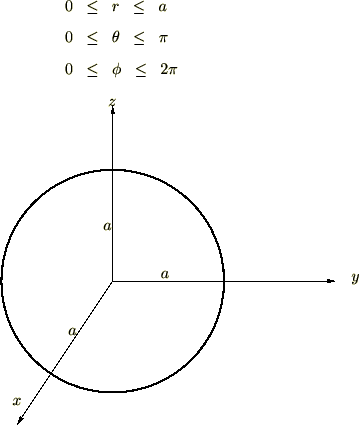
問題③
次に示される底辺が半径![]() の高さが
の高さが![]() の円錐の体積を求めてみましょう。
の円錐の体積を求めてみましょう。
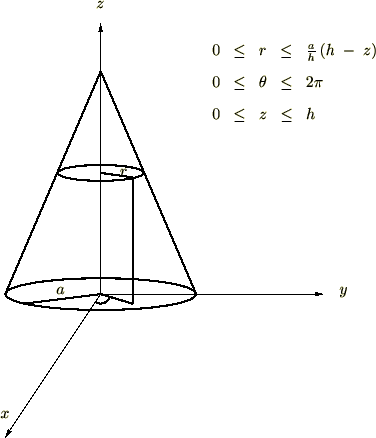
問題④
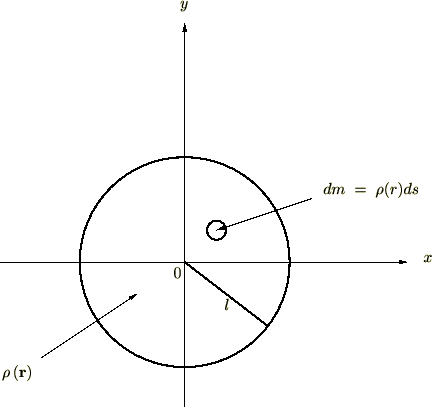
半径が![]() の円盤があるとします。この円盤の密度は中心からの距離の2乗に比例するとします。
の円盤があるとします。この円盤の密度は中心からの距離の2乗に比例するとします。
このような円盤の全質量を求めてみましょう。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
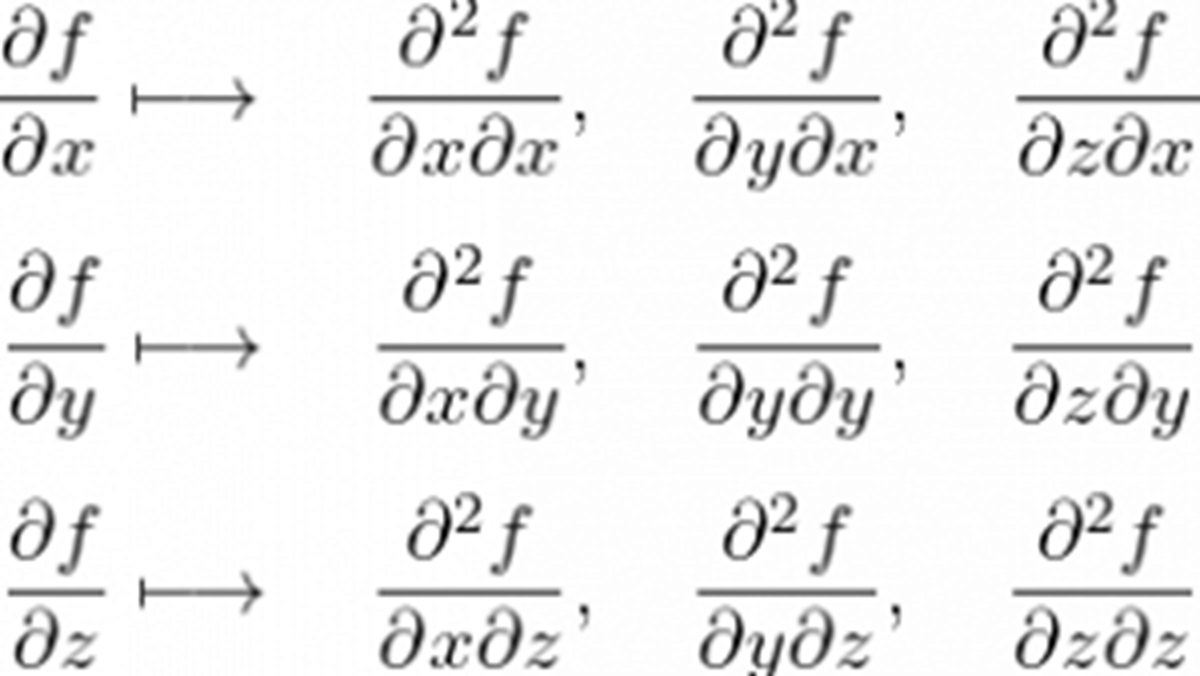
偏微分
続きを読む
-
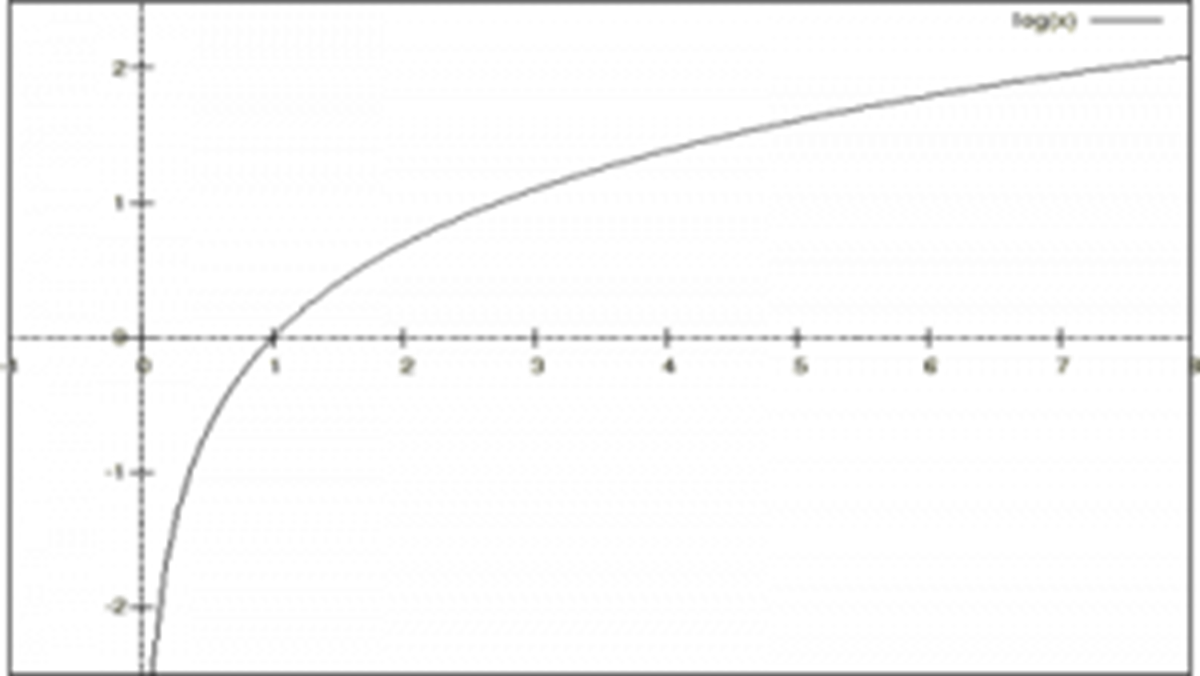
導関数
続きを読む
-

微分積分学
続きを読む
-

長方形板の慣性モーメント
続きを読む
-
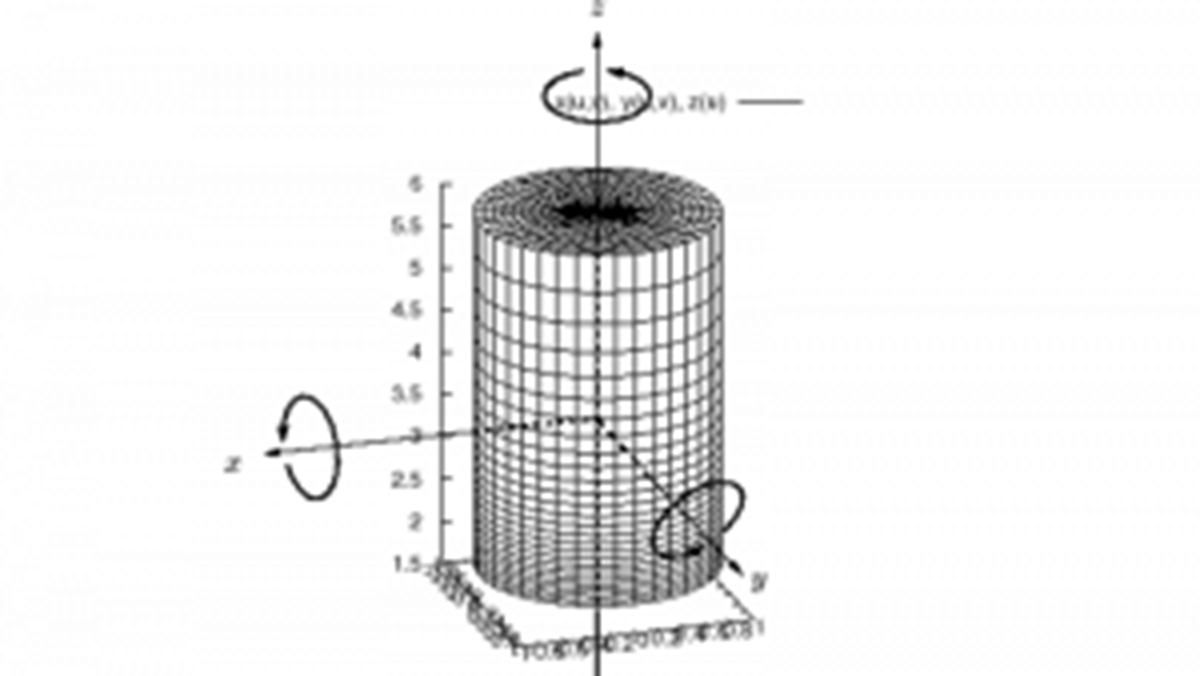
円柱の慣性モーメント
続きを読む
-

半球体の慣性モーメント
続きを読む
-
-
-
-
MOIマイグレーション完全移行完了のお知らせ
カテゴリー : 第2期目マイグレーション完了VPSサーバへの完全移行がとうとう完了しました。2010年代の前半ごろから計画していたものになり、正直行動に移…
-
-
-
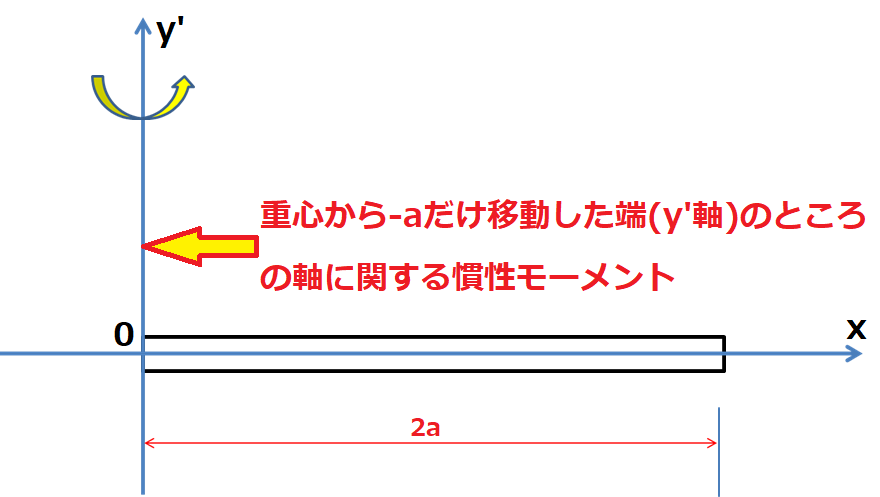
平行軸の定理と棒の慣性モーメント
カテゴリー : 平行軸定理を使った棒の慣性モーメント重心の位置を0とする-aからaまでの棒の距離の長さを2a、棒の左へ-aだけ移動した端を通る軸に関する慣性モーメ…
-
-
-
円錐の頂点、底面、重心に関する慣性モーメント
カテゴリー : 円錐の頂点、底面、重心周りの慣性モーメントこのセクションでは平行軸の定理を利用した円錐の頂点周り、円錐底面に平行で中心点を通る軸周りに関する慣性モーメン…