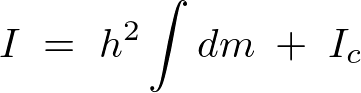剛体の運動
剛体とは
剛体とは任意の2点間の距離が運動しているときに変化しないものをいいます。

さらにこの場合、2点間の距離が変化しないので非相対論的な定義を適用できます。
剛体の運動を考える場合、剛体の空間的な配置がどうなるかはまず空間的位置とその“回転”を決定させる必要があります。

剛体運動を解析するとき解くべき方程式は基本的にこの2つになります。
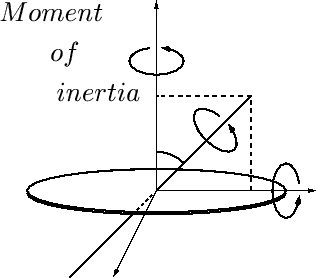
回転軸を持った剛体の回転
| 慣性モーメント(回転慣性を表す) | |
| 外力のモーメント(回転させようとする力) |
と定義すると回転の方程式は次のようなものになります。
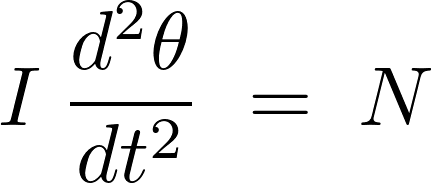
慣性モーメント
三次元中の剛体の運動
回転の方程式とは慣性モーメントのことであり簡単に説明すると回転軸からの距離の2乗にその部分の質量をかけて剛体全体にわたって足しあげたものをいいます。

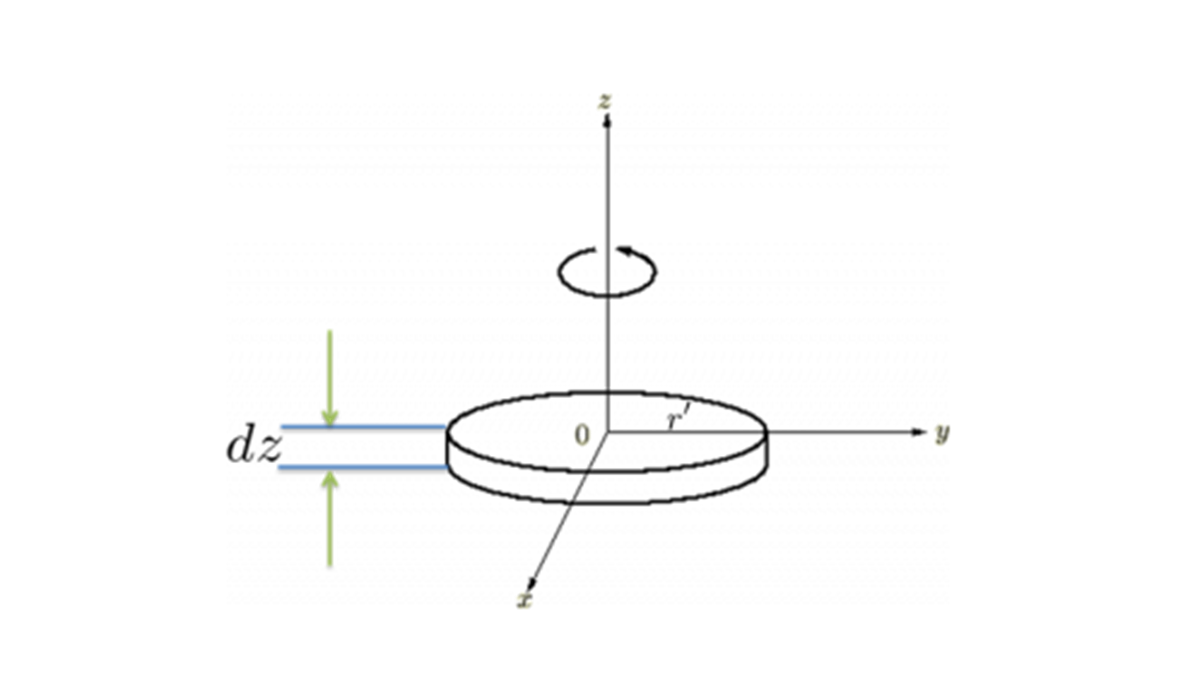
まず剛体中の微小部分![]() を考えます。 この部分と回転軸までの距離を、
を考えます。 この部分と回転軸までの距離を、
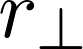
とします。
次に剛体の密度を、
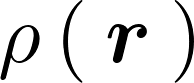
そうすると微小部分の慣性モーメント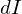 は、
は、
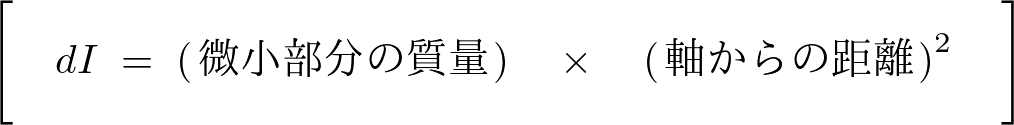
より、以下、
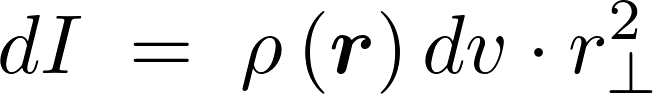
この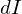 を剛体全体についてたしあげると目的とする慣性モーメントの式になります。
を剛体全体についてたしあげると目的とする慣性モーメントの式になります。
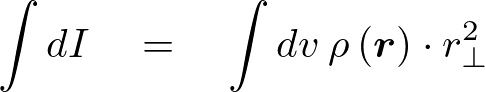
より、
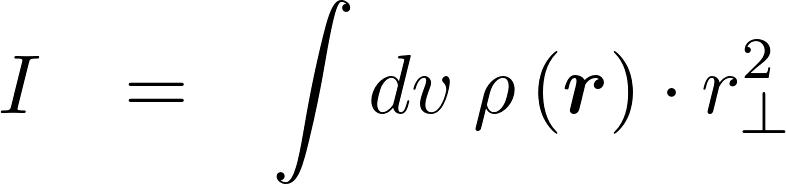
具体的な例【球の慣性モーメント】
具体的な例として球の慣性モーメントについてやってみましょう。
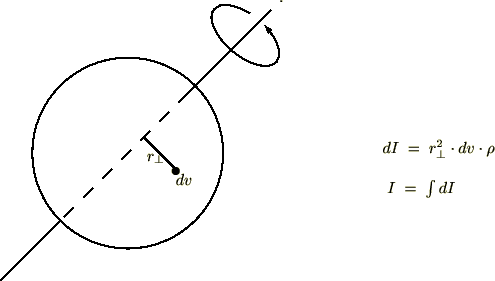
回転軸を![]() にとり半径は
にとり半径は![]() 、おもさを
、おもさを![]() とします。回転軸
とします。回転軸![]() から垂直に伸ばした腕の長さは、
から垂直に伸ばした腕の長さは、
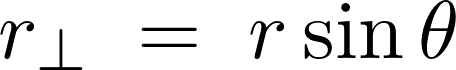
微小体積部分は極座標におけるヤコビアンを使って、

微小部分密度は、
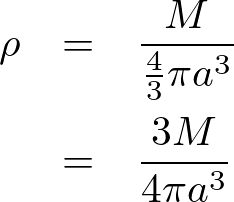
以上により球の微小部分における慣性モーメント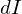 は、
は、

となります。
この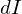 に対し極座標における重積分により全体をたし上げたものが目的とする慣性モーメント
に対し極座標における重積分により全体をたし上げたものが目的とする慣性モーメント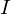 になります。
になります。


Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
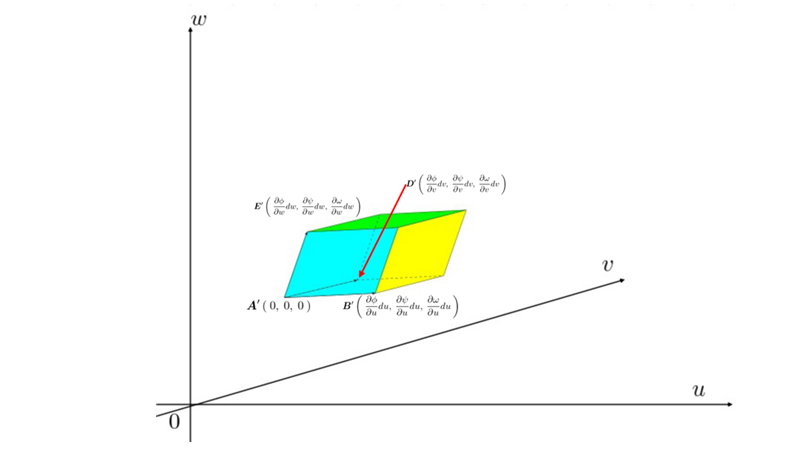
多次元ヤコビアン
続きを読む
-

dv計算法-答え
続きを読む
-

微小体積要素dvの計算
続きを読む
-

MOIマイグレーション完全移行完了のお知らせ
続きを読む
-
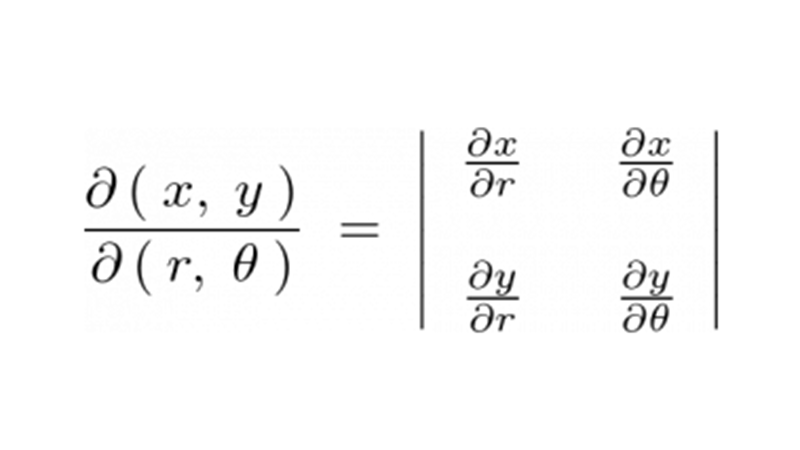
微小面積要素の計算
続きを読む
-

平行軸の定理
続きを読む