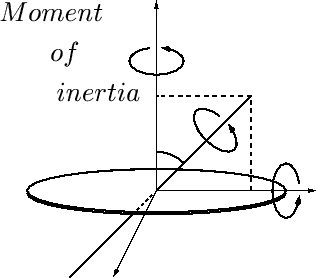
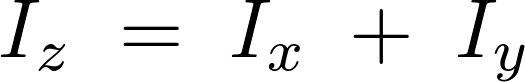円輪の慣性モーメント
円輪の慣性モーメントの導出過程
円輪の中心を通る対称軸に関する慣性モーメントの計算

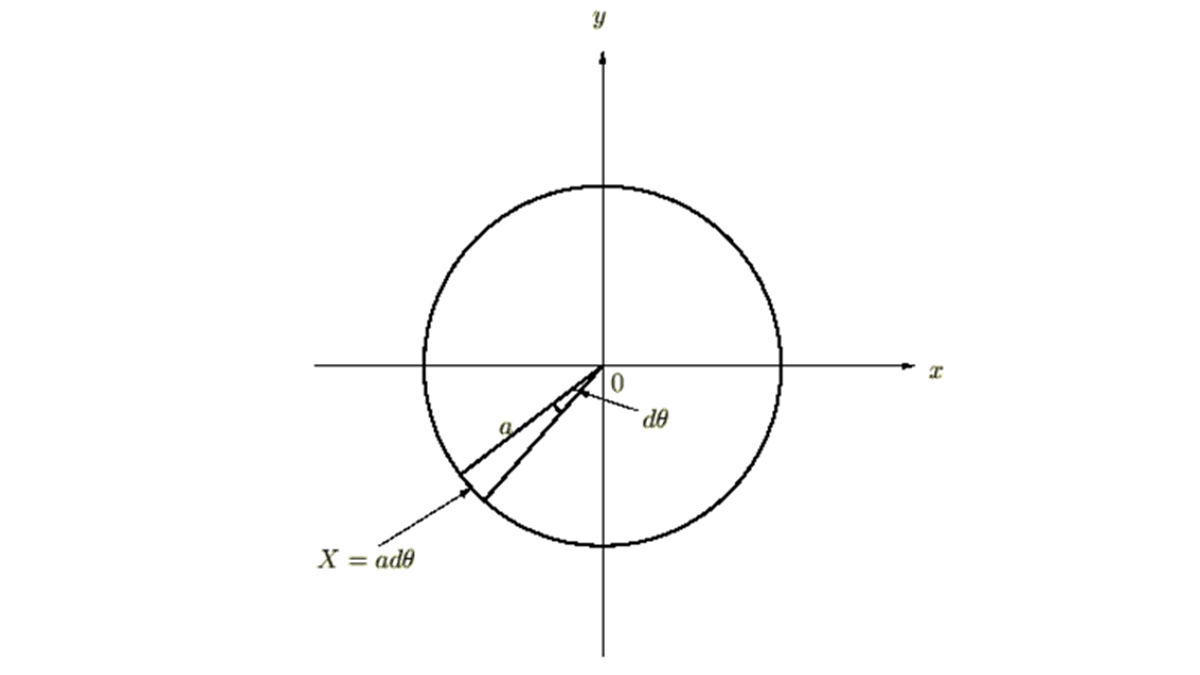
極座標系を取り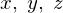 軸周りの慣性モーメントをそれぞれ
軸周りの慣性モーメントをそれぞれ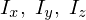 とし、質量は
とし、質量は![]() 、半径は
、半径は![]() 、円周は
、円周は![]() とします。
とします。
なので円輪の線密度は、

角度変数 の微小部分長は
の微小部分長は![]() 。
。
これにより微小部分の質量は、

そして![]() のとる範囲は
のとる範囲は になります。
になります。
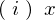 軸まわりの慣性モーメント
軸まわりの慣性モーメント
![]() 軸からの微小部分までの距離は
軸からの微小部分までの距離は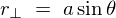 。
。
これらにより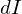 は、
は、

全体にわたってたし上げます。

よって円輪の中心を通る![]() 軸周りの慣性モーメントは以下のようになります。
軸周りの慣性モーメントは以下のようになります。
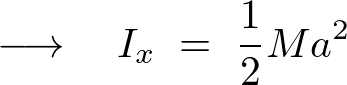
 軸まわりの慣性モーメント
軸まわりの慣性モーメント
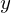 軸からの微小部分までの距離は
軸からの微小部分までの距離は 。
。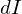 は、
は、
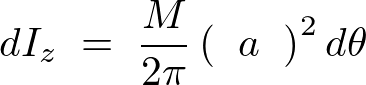
全体にわたってたしあげます。
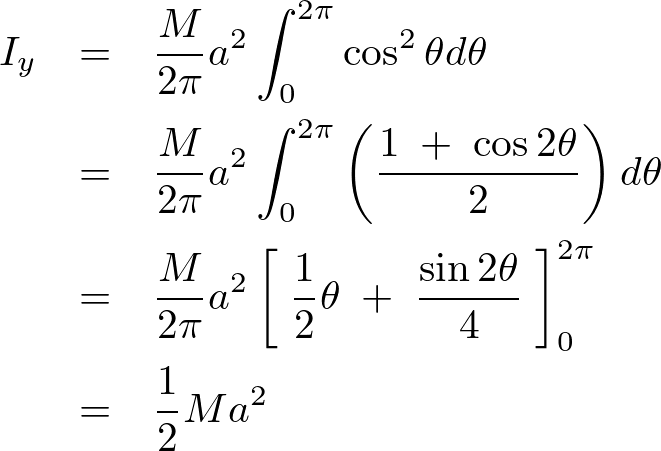
よって円輪の中心を通る![]() 軸周りの慣性モーメントは以下のようになります。
軸周りの慣性モーメントは以下のようになります。
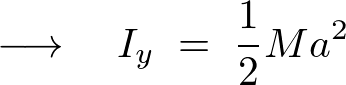
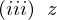 軸周りの慣性モーメント
軸周りの慣性モーメント
![]() 軸からの微小部分までの距離は
軸からの微小部分までの距離は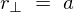 。
。 は、
は、

全体にわたってたしあげます。

となるので円輪の![]() 軸周りの慣性モーメントは以下のようになります。
軸周りの慣性モーメントは以下のようになります。

ちなみにこの円輪に対しても長方形板のときと同じように、次のような関係式が成り立っています。