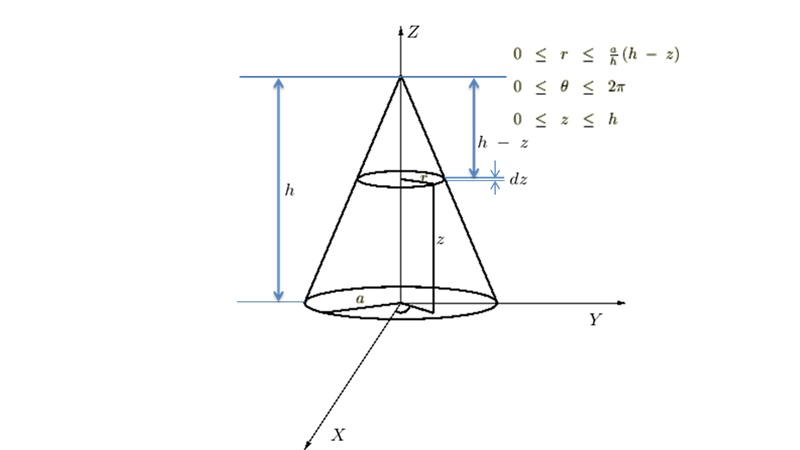
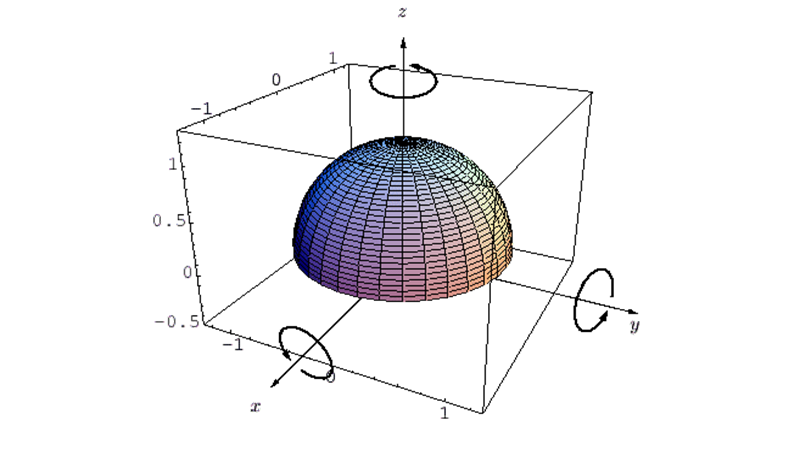
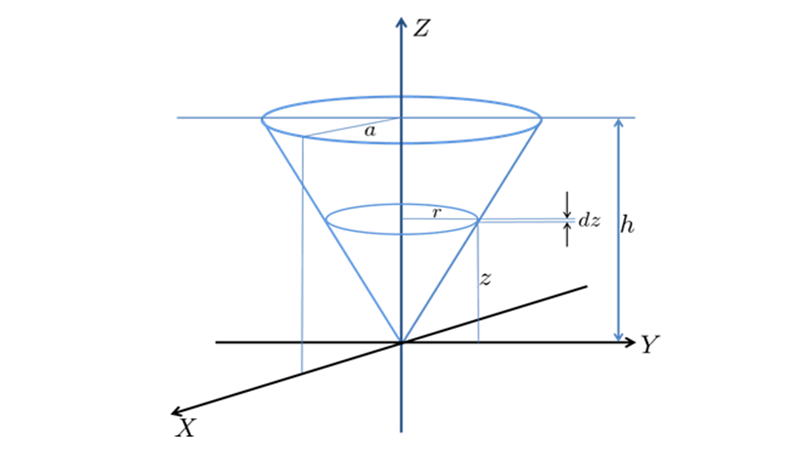
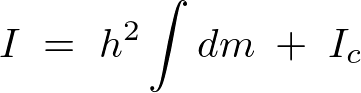半球体の慣性モーメント
半球体の慣性モーメントの導出過程
半球体の重心を通る軸に関する慣性モーメントの導出
【Ⅰ】質量が 、半径が
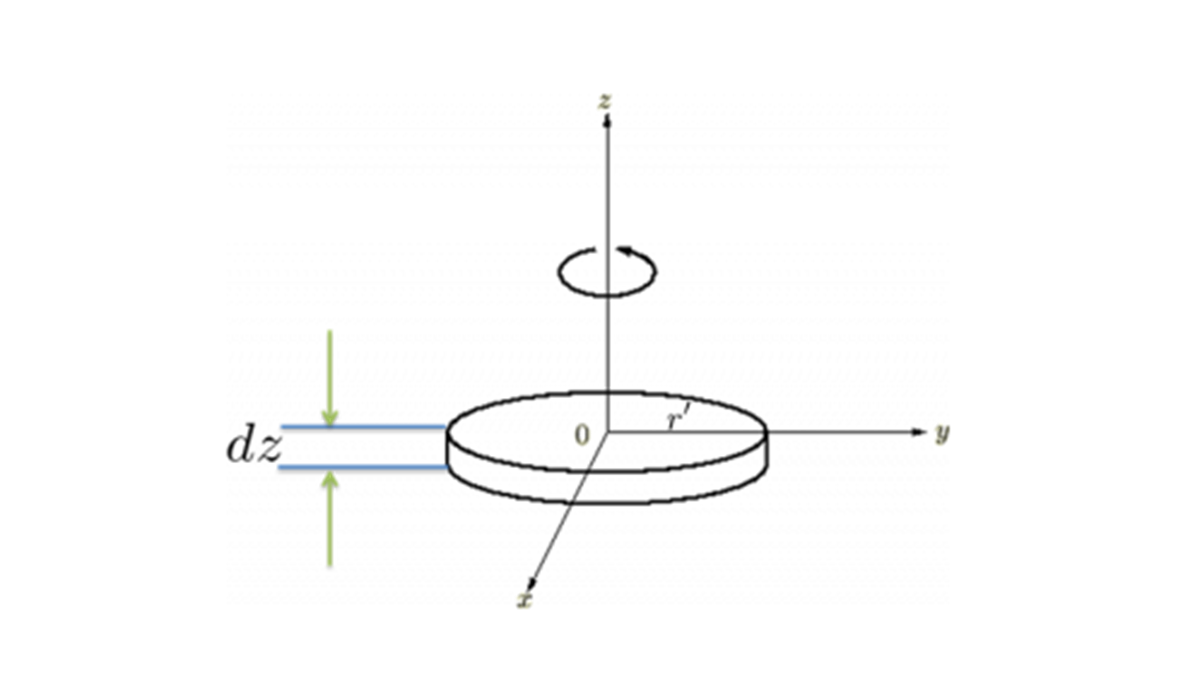
、半径が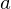 の半円球の重心を通り底面に平行な軸に関する慣性モーメント
の半円球の重心を通り底面に平行な軸に関する慣性モーメント

図の半球体の体積は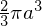 、質量を
、質量を![]() とします。
とします。
体積密度は、
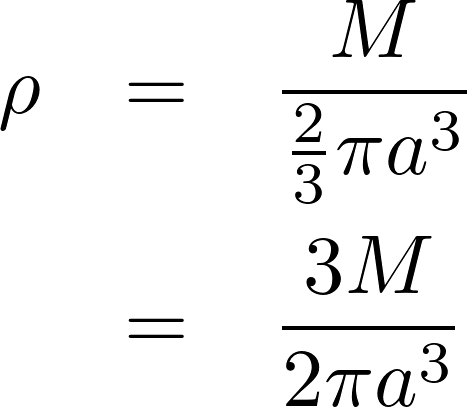
回転軸(![]() 軸とします)からの距離は、
軸とします)からの距離は、
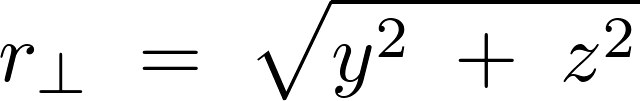
極座標を使えば、
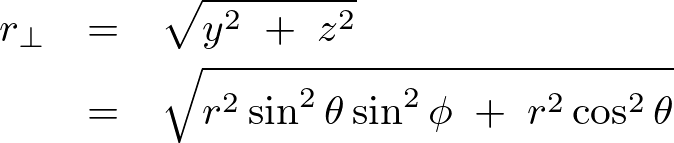
これらにより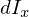 は、
は、
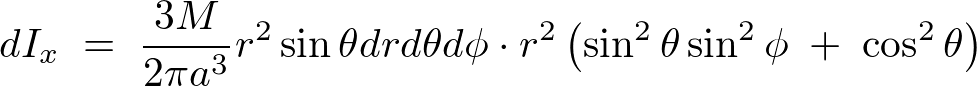
たし上げます。

よって半球体における半径が![]() の半円球の重心を通り底面に平行な
の半円球の重心を通り底面に平行な![]() 軸周りの慣性モーメントは以下のようになります。
軸周りの慣性モーメントは以下のようになります。

ちなみに上記計算途中の式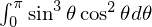 の積分はチャプター1に出てきた三角関数の積分公式を適用し次のように計算しています。
の積分はチャプター1に出てきた三角関数の積分公式を適用し次のように計算しています。


【Ⅱ】半円級の重心を通る対称軸に関する慣性モーメント

半径を![]() とし
とし![]() 軸を回転軸とします。
軸を回転軸とします。
この時の半円球に関しての慣性モーメントを導いていきます。
回転軸からの距離は、

体積密度は先ほどと同じなので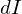 は、
は、
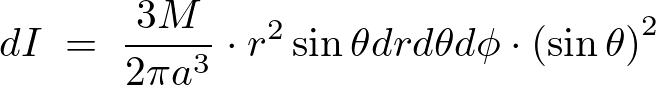
積分範囲に気を付けてこれをたし上げます。

よって以下のように求まります。

-
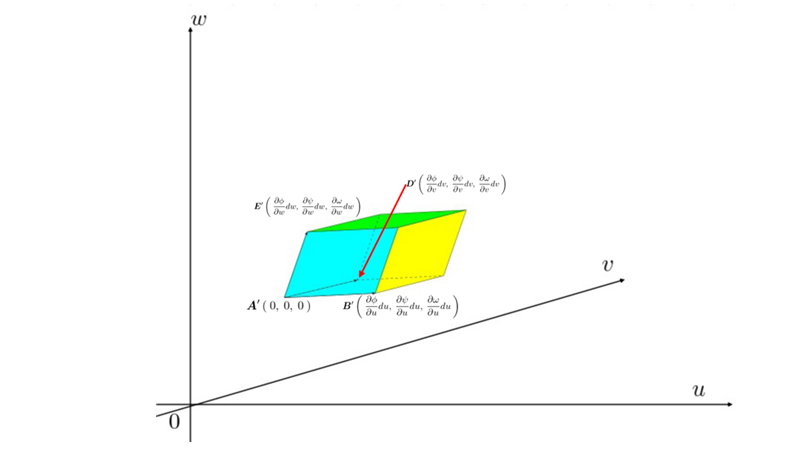
多次元ヤコビアン
続きを読む
-

dv計算法-答え
続きを読む
-

微小体積要素dvの計算
続きを読む
-

MOIマイグレーション完全移行完了のお知らせ
続きを読む
-
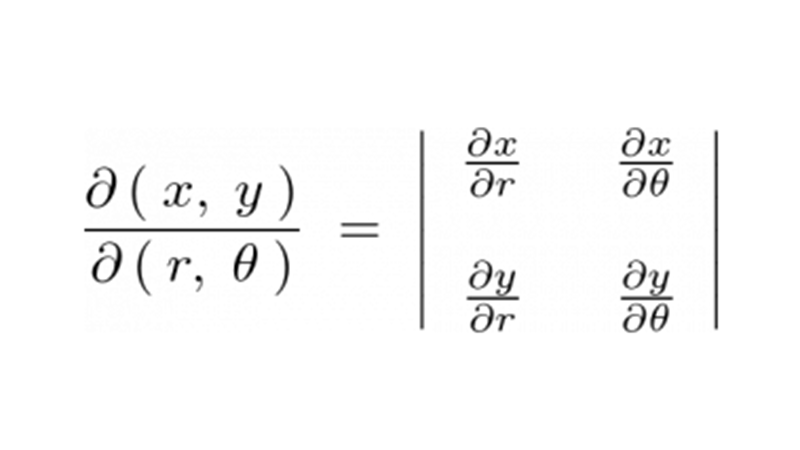
微小面積要素の計算
続きを読む
-

平行軸の定理
続きを読む