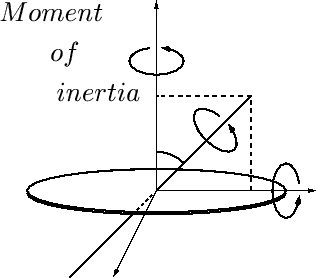
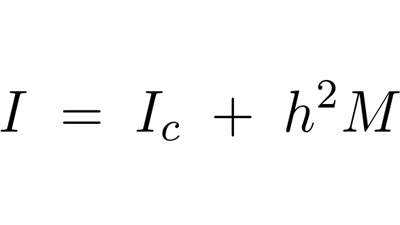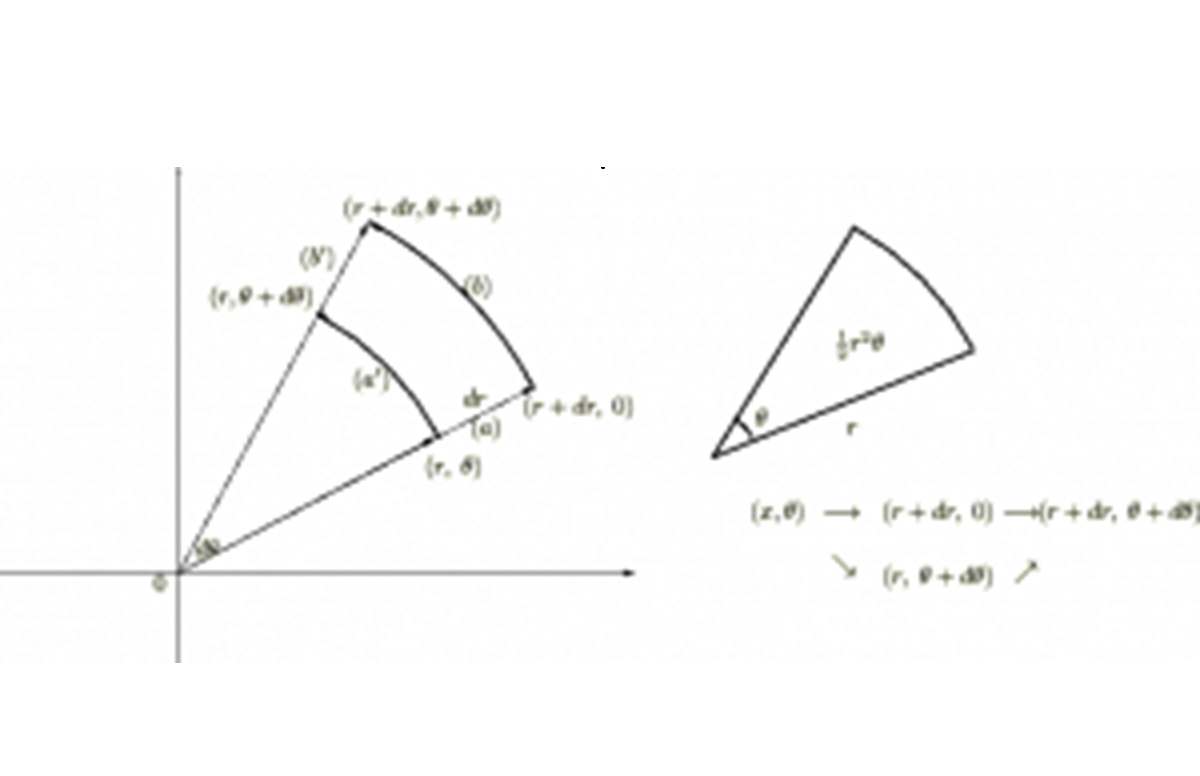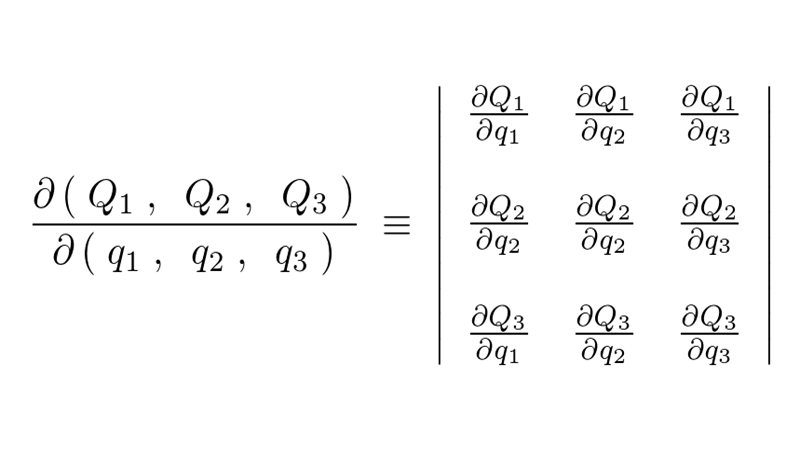平行軸定理と慣性モーメント
平行軸の定理とは
任意の点0を通る 軸のまわりの慣性モーメントの計算
軸のまわりの慣性モーメントの計算
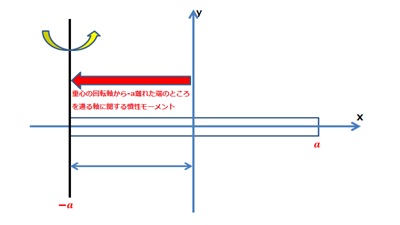
重心を通る1つの軸があるとし、それを![]() 軸として、
軸として、![]() 軸の周りの剛体の慣性モーメントを
軸の周りの剛体の慣性モーメントを とします。 この軸に平行で
とします。 この軸に平行で![]() の距離を隔てた軸まわりの慣性モーメントを考えてみましょう。
の距離を隔てた軸まわりの慣性モーメントを考えてみましょう。

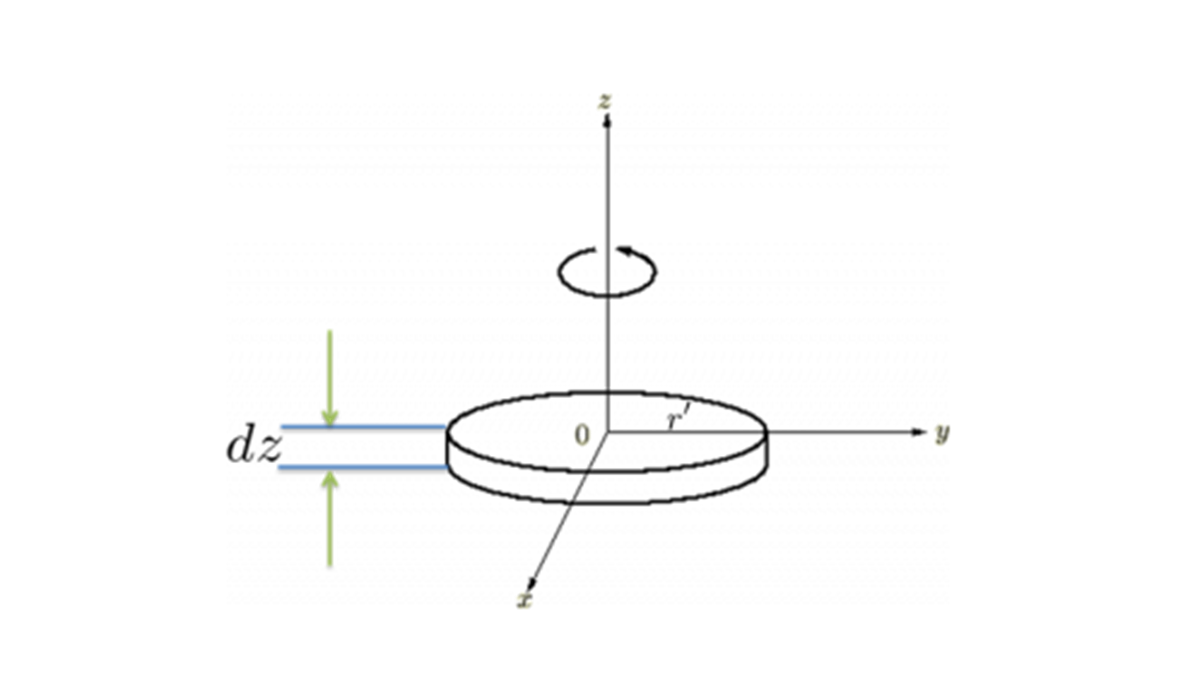
の式を積分の形にすれば、

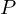 点の
点の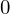 の周りのモーメントは、
の周りのモーメントは、
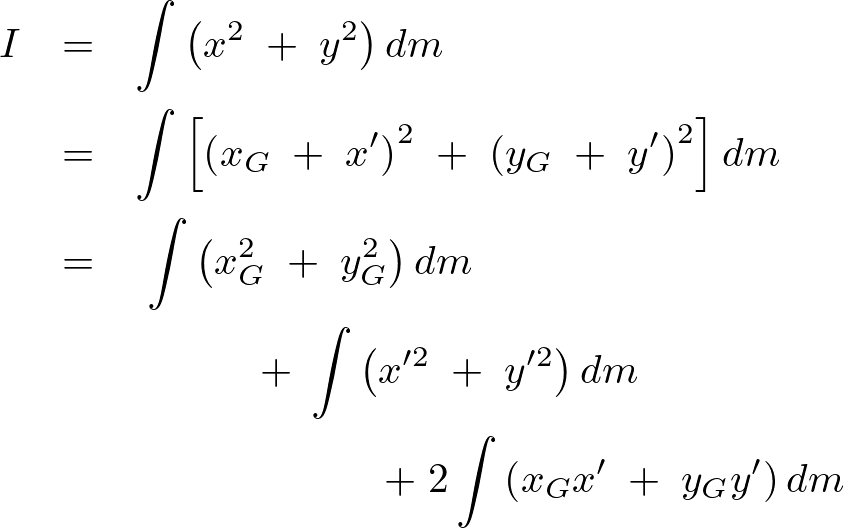
ここで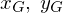 を質量中心の座標とします。
を質量中心の座標とします。
積分の第2項は質量中心を通り、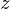 軸に平行な軸周りの慣性モーメントであり、これを
軸に平行な軸周りの慣性モーメントであり、これを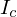 とします。
とします。
質量中心より回転の中心 までの距離を
までの距離を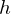 とすると、
とすると、
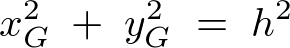
さらに第3項の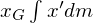 及び
及び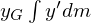 は質量中心の定義においてゼロ。
は質量中心の定義においてゼロ。
以上の結果より、慣性モーメントとして、
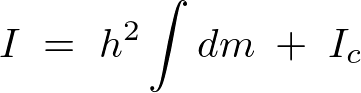
すなわち、

が導かれることになります。
この定理は様々な形でよく利用されるものであり、はじめのうちは何かとややこしく感じますが使い慣れてくると非常に役に立つ便利なものになります。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.