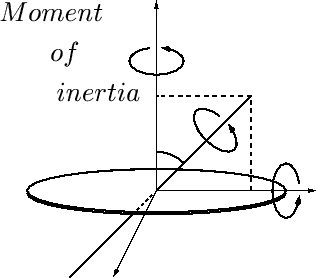
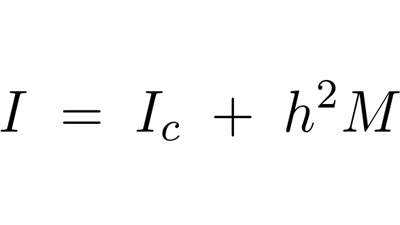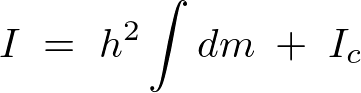平行軸定理の簡単な例
平行軸の定理を利用した慣性モーメントの簡単な計算例
簡単な例として棒の慣性モーメントを取り上げます。
重心の位置を![]() とする
とする![]() から
から![]() までの棒の距離の長さを
までの棒の距離の長さを![]() 、質量
、質量![]() の一様な棒の左へ
の一様な棒の左へ![]() だけ移動した端を通る軸に関する慣性モーメントをこの平行軸の定理を使って求めます。
だけ移動した端を通る軸に関する慣性モーメントをこの平行軸の定理を使って求めます。
端点に関する慣性モーメントの直接の導出
まず最初に平行軸の定理を使わない形での端点に関する棒の慣性モーメントを求めてみます。
重心の位置を![]() としています。
としています。
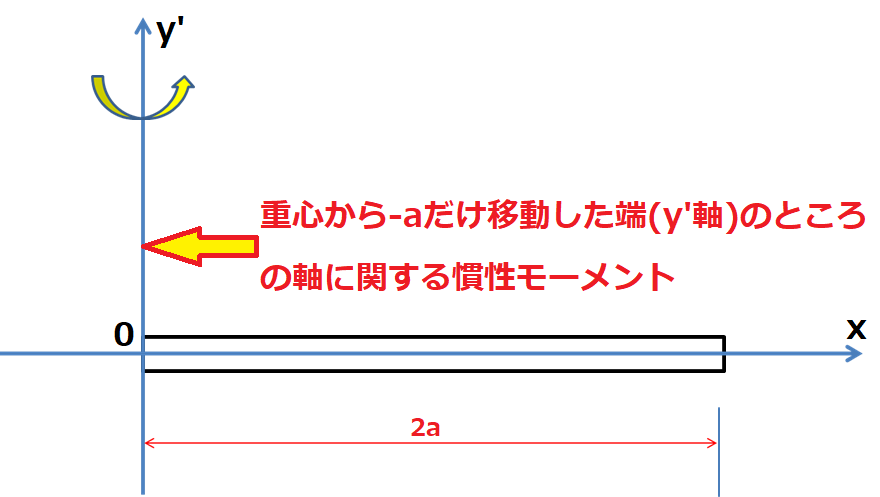
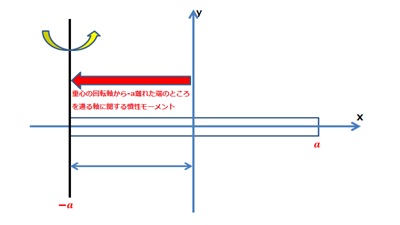
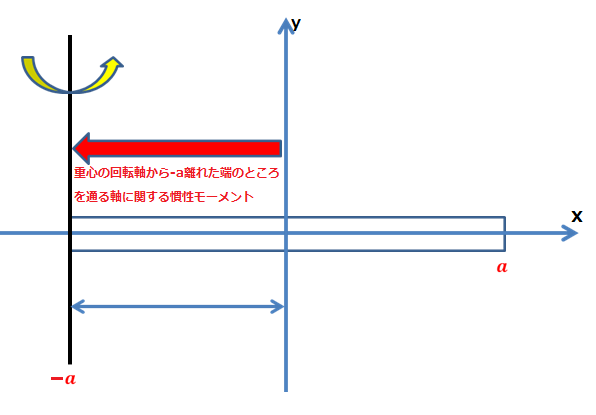
座標系は回転軸を![]() とする
とする![]() 軸をとり、上図より回転軸y’軸より長さ
軸をとり、上図より回転軸y’軸より長さ![]() の一様な質量Mの棒の慣性モーメントに関する棒の中心軸ではない端の部分の慣性モーメントを求めてみます。
の一様な質量Mの棒の慣性モーメントに関する棒の中心軸ではない端の部分の慣性モーメントを求めてみます。
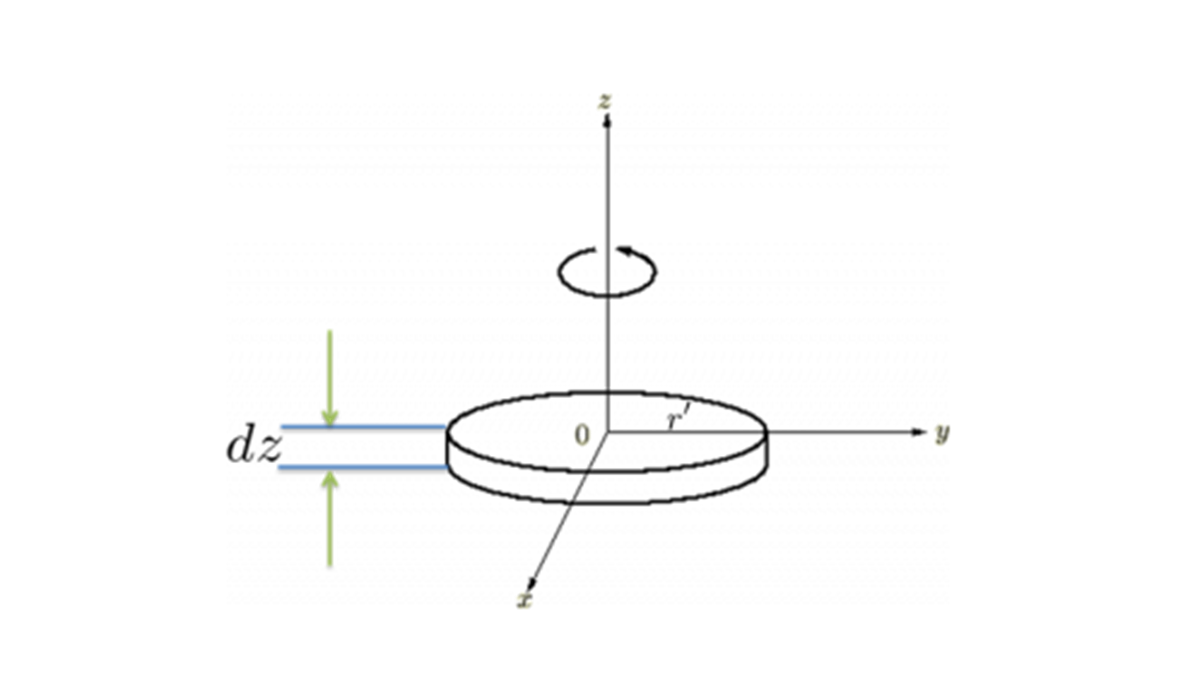
微小部分の長さは、
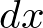
微小線要素部分の密度は、
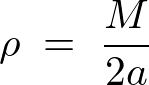
これにより微小部分の体積密度は、
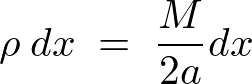
回転軸からの距離に関する積分範囲は、
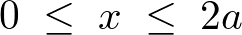
さらに回転軸から任意の微小部分への距離は、
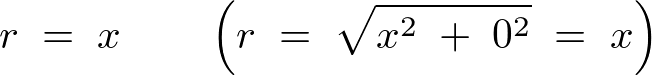
となるので微小線要素部分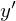 は以下のようになります。
は以下のようになります。
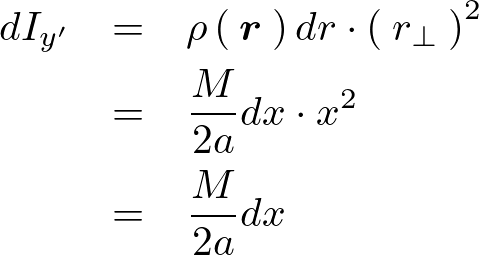
これを積分範囲の![]() から
から![]() まで足し上げます。
まで足し上げます。
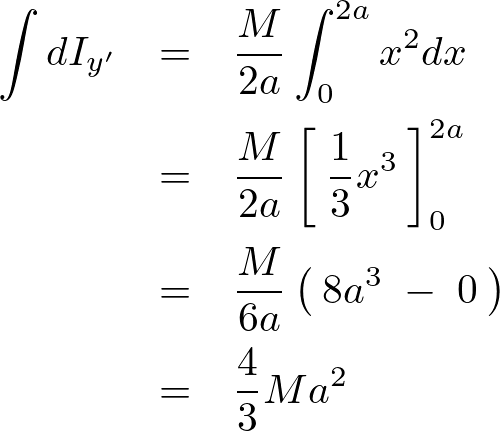
となるので端点における棒の慣性モーメントの結果はひとまず以下のようになります。
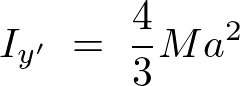
平行軸の定理を使った慣性モーメントの導出過程
新たに以下のように重心を通る中心軸に関する軸を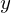 軸として以下のように座標系を置きます。
軸として以下のように座標系を置きます。
まずこの棒の重心軸に関する慣性モーメントを求めると次のようになります。
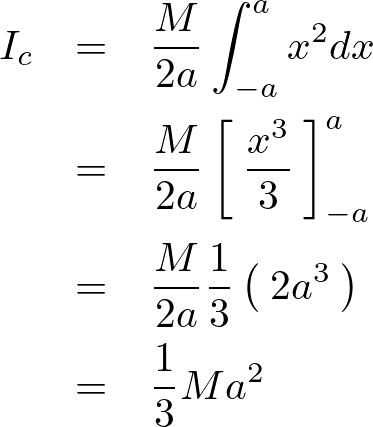
一様な棒の重心に関する慣性モーメントの詳しい導出過程はこちら
これを平行軸の定理に代入すると、
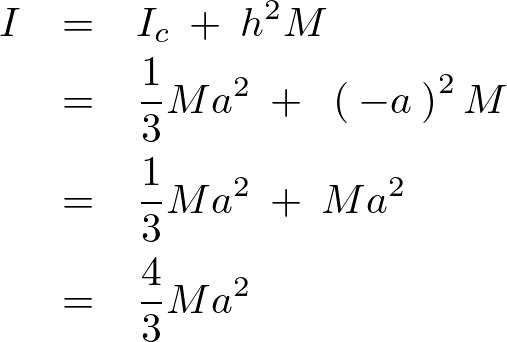
よって棒の中心軸から離れた端を通る位置に関する慣性モーメント以下のように求まります。
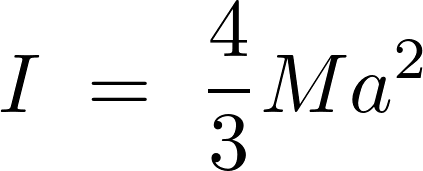
平行軸の定理を使わず直接求めた端点における慣性モーメントの結果と同じになります。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
平行軸の定理と棒の慣性モーメント
カテゴリー : 平行軸定理を使った棒の慣性モーメント重心の位置を0とする-aからaまでの棒の距離の長さを2a、棒の左へ-aだけ移動した端を通る軸に関する慣性モーメ…