1変数関数の積分
1変数関数の積分

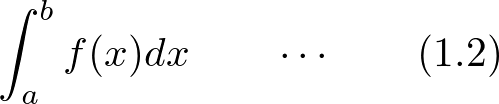
(1.1)を不定積分、(1.2)のほうを定積分といいます。最初の部分にでている“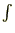 ”はインテグラルといい積分そのものを意味します。
”はインテグラルといい積分そのものを意味します。 が被積分関数であり、
が被積分関数であり、![]() はこの場合
はこの場合![]() で積分しなければならないということを意味しています。
で積分しなければならないということを意味しています。
基本としては何で(どういった記号で)積分するかは大して重要ではなく上記の![]() という記号でなければ例えば
という記号でなければ例えば![]() といった記号を使っても構いません。つまり、
といった記号を使っても構いません。つまり、
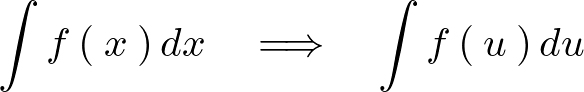
と書いても意味は同じです。
ちなみに定積分が面積や長さを調べるものであり、それに対し不定積分は微分方程式などに使われます。
ある点![]() を考え
を考え![]() を含む微小区間
を含む微小区間![]() を考えます。
を考えます。 における関数値は
における関数値は です。よって
です。よって は下図における短冊の面積と考えればよいでしょう。
は下図における短冊の面積と考えればよいでしょう。

この短冊の面積を考えれば![]() は次のようにして求められます。
は次のようにして求められます。
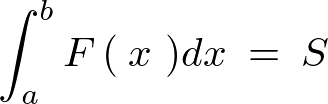
例題

![]() というのは
というのは![]() のイニシャルであり積分定数のことです。
のイニシャルであり積分定数のことです。
不定積分公式
以下は主な公式です。このへんは記憶しておくとあとあと便利だと思います。

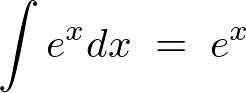
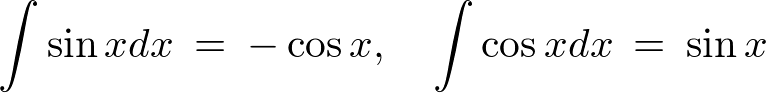
置換積分
積分の変数変換
積分の計算というのは、主に積分の公式が使えるように変形させるという行為が非常に重要になってきます。
例えば次のような形の積分はどう行えばよいでしょうか?
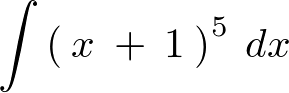
こういったものの場合、ほかのある変数で置き換える(置換)という作業をします。
上記の問題ではまず括弧の中の![]() に着目してそれを仮に
に着目してそれを仮に![]() とおきます。
とおきます。
それを![]() で微分すると、
で微分すると、
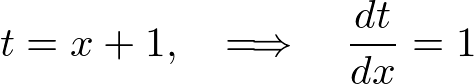
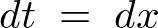
となるのでこれらを元の式に代入すれば、
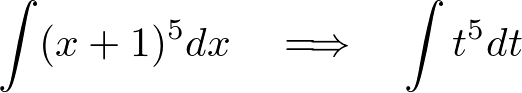
となります。これを普通に積分して元に戻せば、
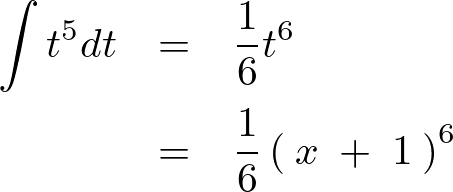
以下のような指数関数に関する積分を先ほどの置換積分を用いて解いてみましょう。
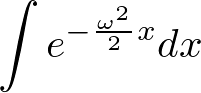
答え
まず乗数部分を次のようにおきます。
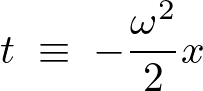
これを![]() で微分します。
で微分します。
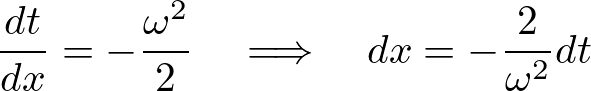
代入します。
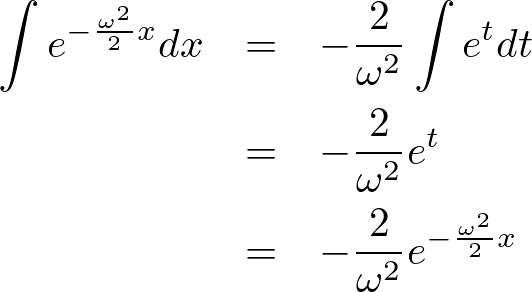
部分積分法
公式としては次のようになります。
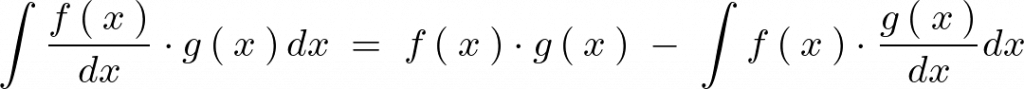
このとき![]() が
が![]() にあたり、
にあたり、![]() が
が![]() に相当します。
に相当します。
なのでまず![]() を求めなければならないので
を求めなければならないので![]() を積分します。
を積分します。
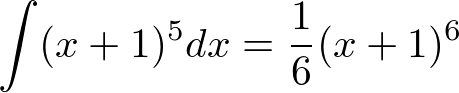
これを部分積分の公式に入れていくと、
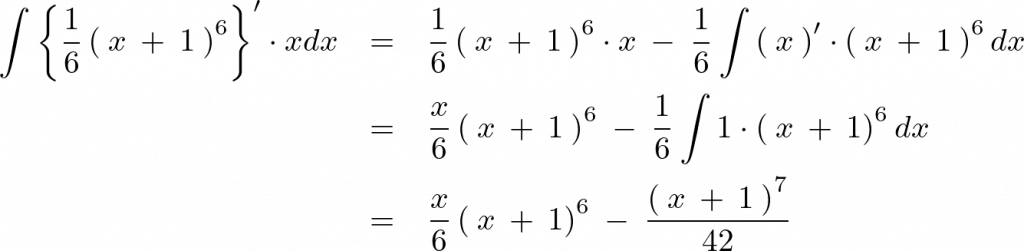
問題
次に示す不定積分を部分積分によって解いてみましょう。
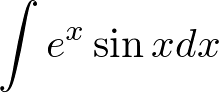
答え
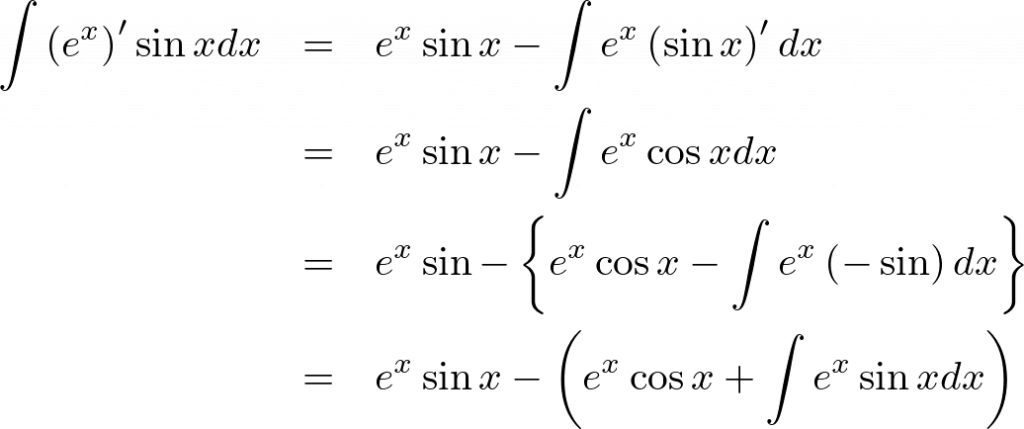
ここで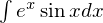 を
を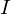 と置きましょう。
と置きましょう。
すると、
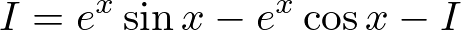
より、
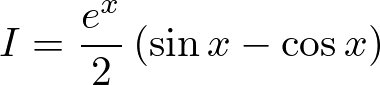
定積分
例題
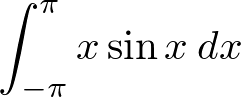
部分積分法を使います。
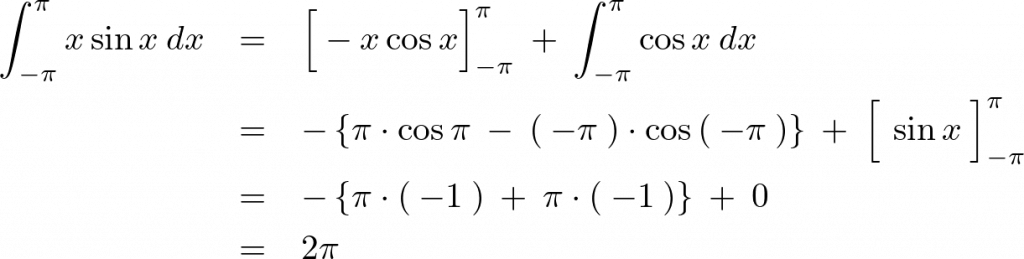
ちなみに![]() の性質上、
の性質上、![]() は
は![]() です。
です。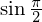 だと
だと![]() です。
です。
こういったことは記憶ではなく、頭の中に次に示すような単位円を思い浮かべるとわかりやすいかと思います(理由は自分で考えてみましょう)。
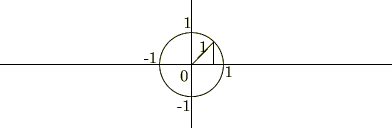
三角関数の積分公式
球の慣性モーメントを計算する際に次に示すような三角関数の積分計算が必要になります。
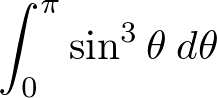
三角関数の公式として次のようなものがあります。
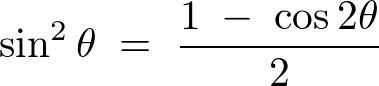
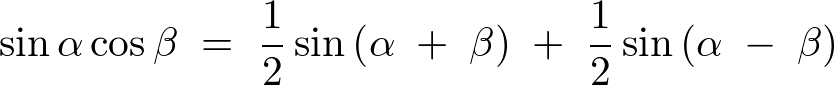
これらを当てはめれば、
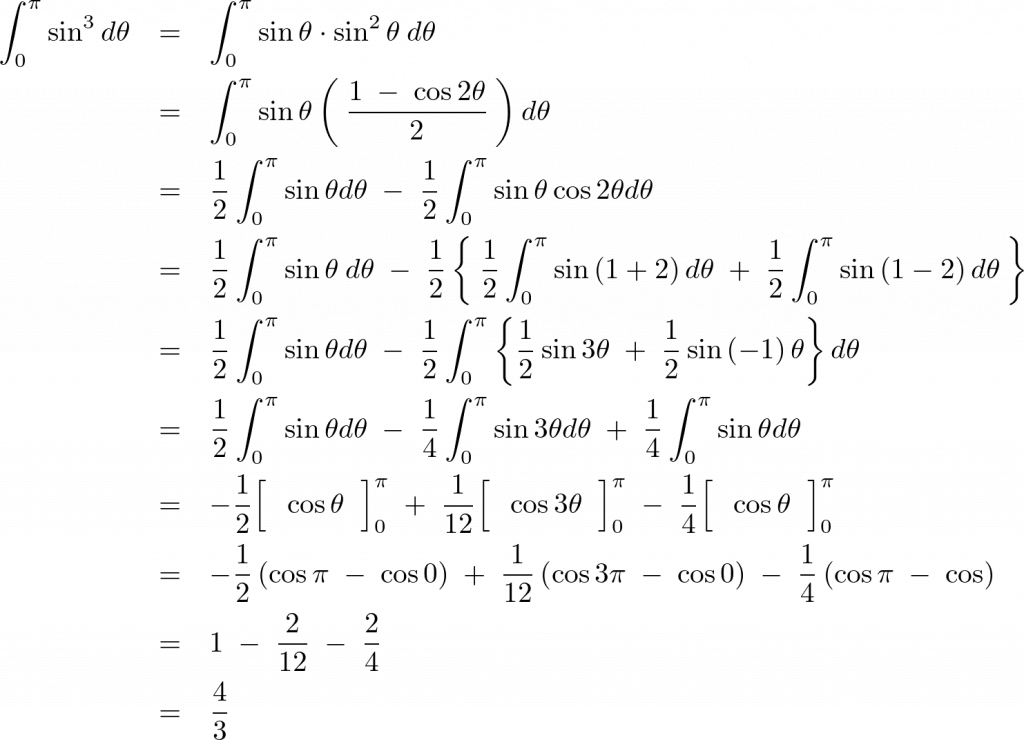
また上記の方法以外にも次に示されるような三角関数の積分公式があります。
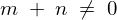 かつ、
かつ、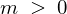 のとき、
のとき、
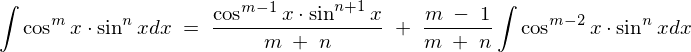
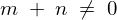 かつ
かつ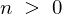 のとき、
のとき、
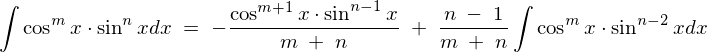
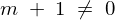 かつ、
かつ、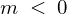 のとき、
のとき、
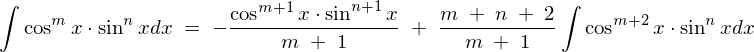
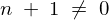 かつ、
かつ、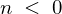 のとき、
のとき、
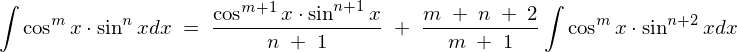
上記の公式を使って実際にやってみると、
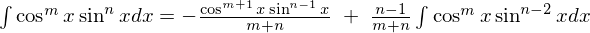
の式にそれぞれ当てはめていけば。
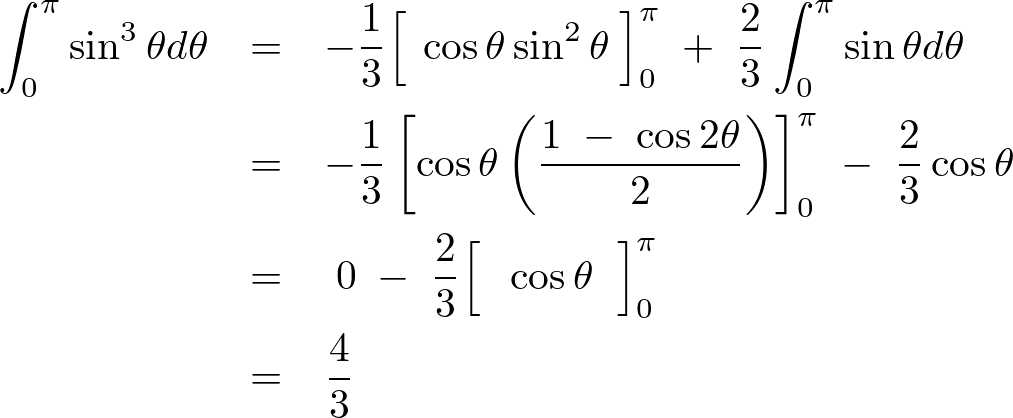

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.