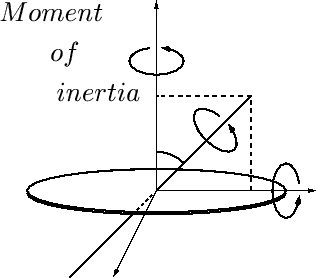
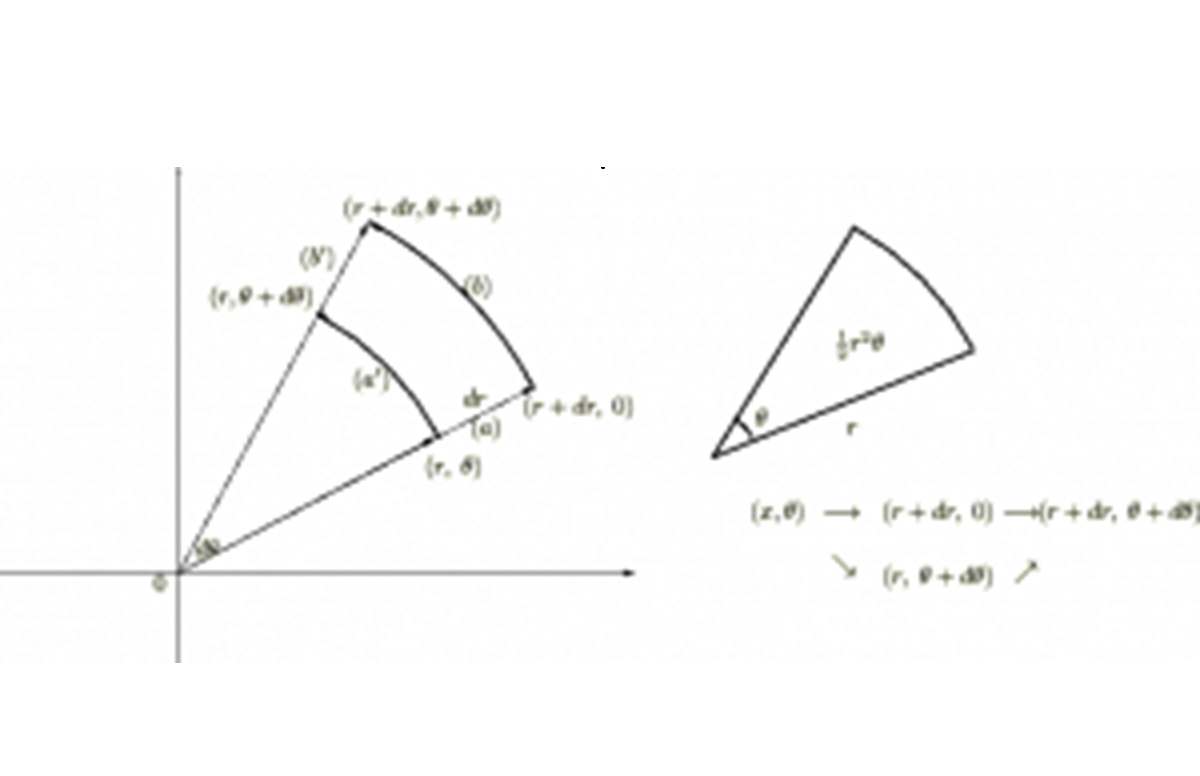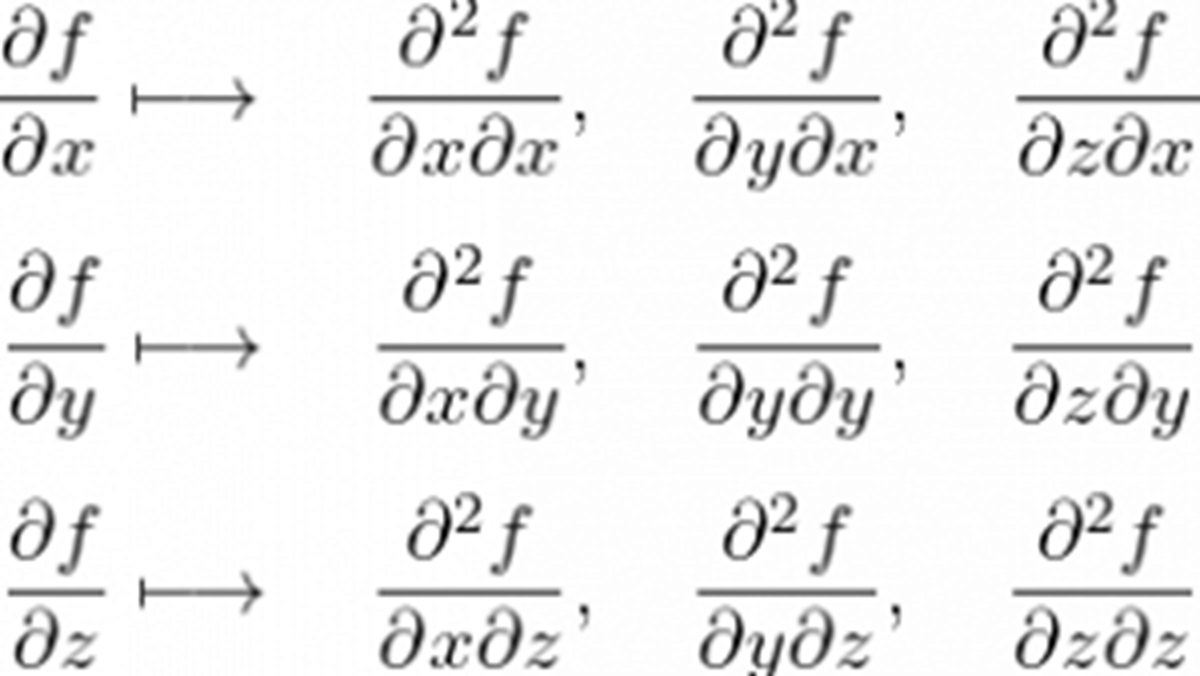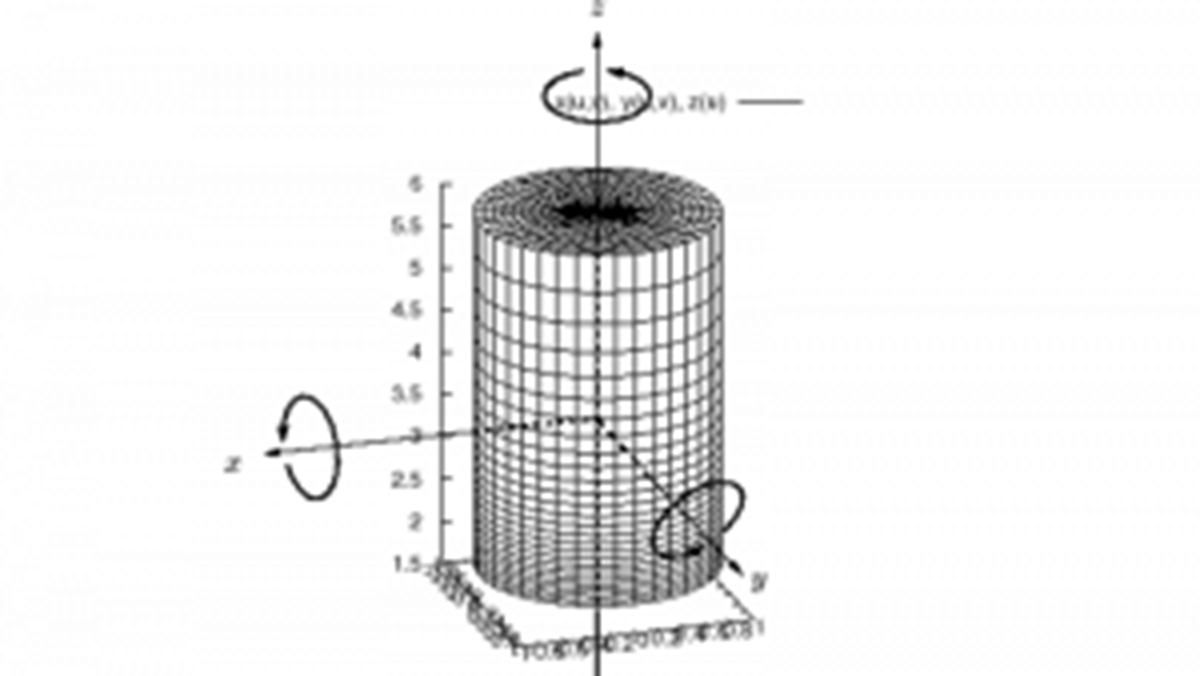平行軸の定理と慣性モーメント
このチャプターは“平行軸の定理”で学習した内容の応用編になります。
平行軸の定理とは、物体の軸に関しての慣性モーメントがわかっているとき、これに平行な位置における軸に関しての慣性モーメントを求めるとき使われる計算法になります。
平行軸の定理に関してのおさらい
任意の点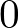 を通る
を通る 軸の周りの慣性モーメントの計算
軸の周りの慣性モーメントの計算
重心を通る1つの軸があるとし、それを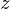 軸として、
軸として、![]() 軸の周りの剛体の慣性モーメントを
軸の周りの剛体の慣性モーメントを とします。この軸に平行で
とします。この軸に平行で![]() の距離を隔てた軸まわりの慣性モーメントを考えると、
の距離を隔てた軸まわりの慣性モーメントを考えると、

の式を積分の形にすれば、

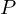 点の
点の の周りのモーメントは、
の周りのモーメントは、
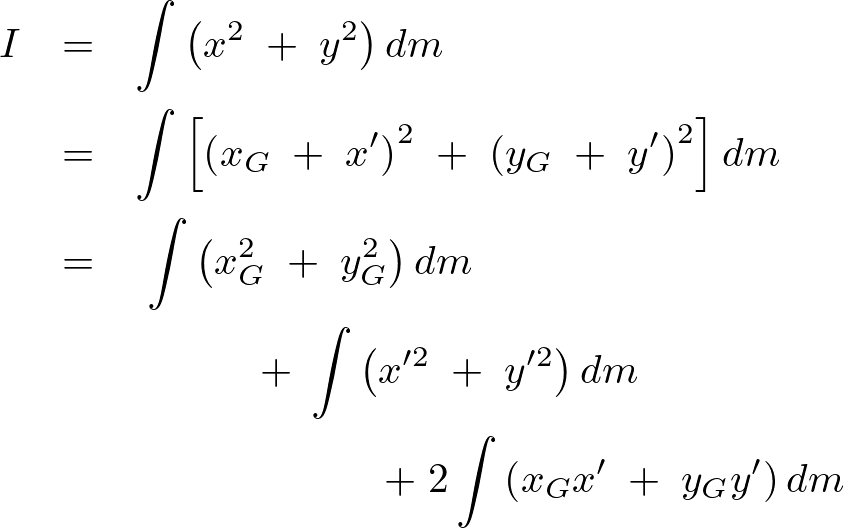
ここで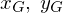 を質量中心の座標とします。
を質量中心の座標とします。
積分の第2項は質量中心を通り、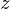 軸に平行な軸周りの慣性モーメントであり、これを
軸に平行な軸周りの慣性モーメントであり、これを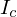 とします。
とします。
質量中心より回転の中心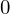 までの距離を
までの距離を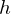 とすると、
とすると、
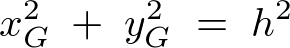
さらに第3項の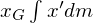 及び
及び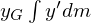 は質量中心の定義においてゼロ。
は質量中心の定義においてゼロ。
以上の結果より、慣性モーメントとして、
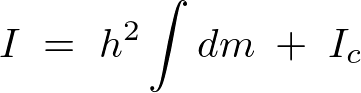
すなわち、

が導かれることになります。
このチャプターではこの平行軸の定理を利用した応用編となっています。
以下のコンテンツよりお入りください。

くり抜き円慣性モーメント
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

円錐の慣性モーメント
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
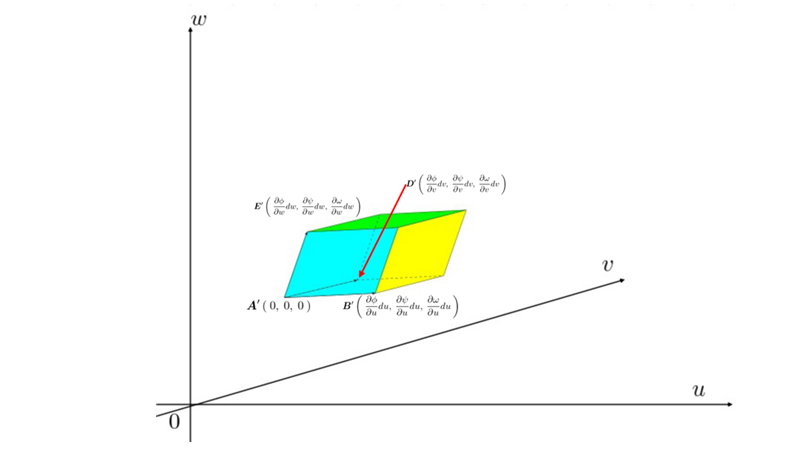
多次元ヤコビアン
カテゴリー
-

dv計算法-答え
カテゴリー
-

微小体積要素dvの計算
カテゴリー
-

MOIマイグレーション完全移行完了のお知らせ
カテゴリー
-
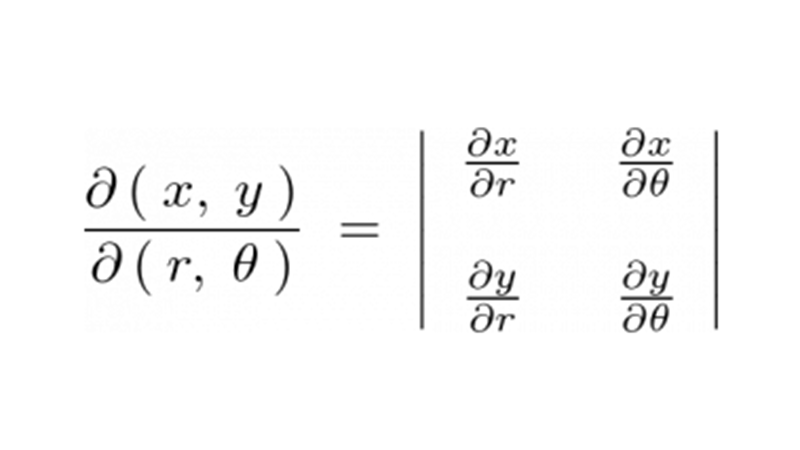
微小面積要素の計算
カテゴリー
-

平行軸の定理
カテゴリー
-
円錐の頂点、底面、重心に関する慣性モーメント
カテゴリー : 円錐の頂点、底面、重心周りの慣性モーメントこのセクションでは平行軸の定理を利用した円錐の頂点周り、円錐底面に平行で中心点を通る軸周りに関する慣性モーメン…
-