問題
初めに（20210619）
当サイトを参考にしてサイト及び動画(youtube)作成・運営している方へのお願い
【社会人として最低限のルール、マナーは守りましょう】
近年、当ドメインコンテンツの明らかな盗用と思われるサイト・動画が一部散見されます。
参考にしたのであれば紹介リンクなどの注釈を入れるといった対応は必ずお願いいたします。
問題①
次に示す直方体の体積を三重積分によって求めてみましょう。
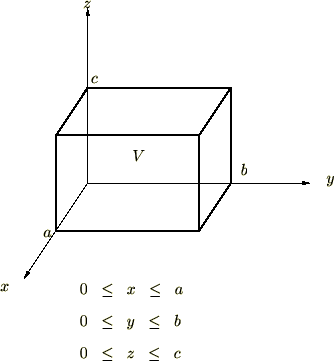
問題②
半径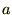
の球の体積を極座標で求めてみましょう。
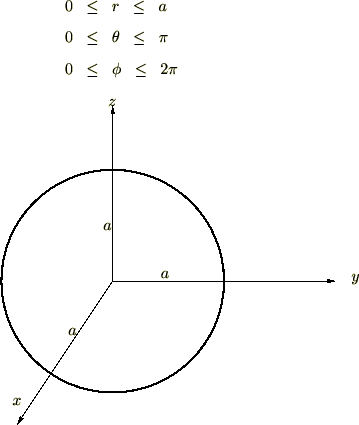
問題③
次に示される底辺が半径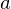
の高さが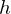
の円錐の体積を求めてみましょう。
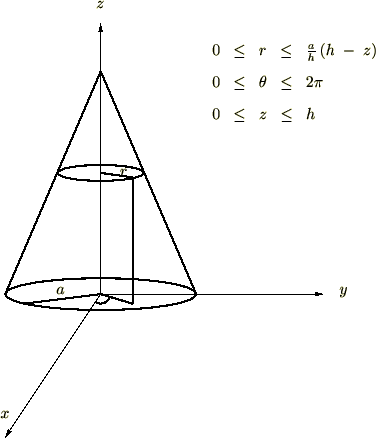
問題④
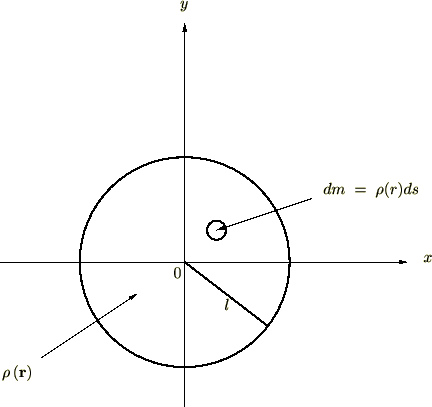
半径が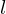
の円盤があるとします。この円盤の密度は中心からの距離の２乗に比例するとします。
このような円盤の全質量を求めてみましょう。
ｄｖ計算の問題関連ページ
- 変数変換とヤコビアン(作成中)
- ある座標系を他の座標系へ変換するときに関数行列式をいうのを用います。この時の関数行列式をヤコビアンと呼びます。ここではこのヤコビアンに関してその意味を考察していきます。
- 微小面積要素の計算
- ある座標系を他の座標系へ変換するときに関数行列式をいうのを用います。この時の関数行列式をヤコビアンと呼びます。このヤコビアンを使って実際にデカルト座標系から極座標、さらには円柱座標系への変換を、偏微分や行列計算を行って求めます。
- dvの計算法
- 慣性モーメントとは、簡単に説明すれば物体（剛体）の回転のしづらさ、回りだす変化のしにくさを示す物体の物理的な特性のことだと考えることができるでしょう。またさらに別の言い方をすれば回転の方程式といえるかもしれません。このサイトは主にこの慣性モーメントの導出の仕方と計算法を中心に解説した内容になっています。
- 答え
- ある座標系を他の座標系へ変換するときに関数行列式をいうのを用います。この時の関数行列式をヤコビアンと呼びます。このヤコビアンを使って実際にデカルト座標系から極座標、さらには円柱座標系への変換を、偏微分や行列計算を行って求めます。
